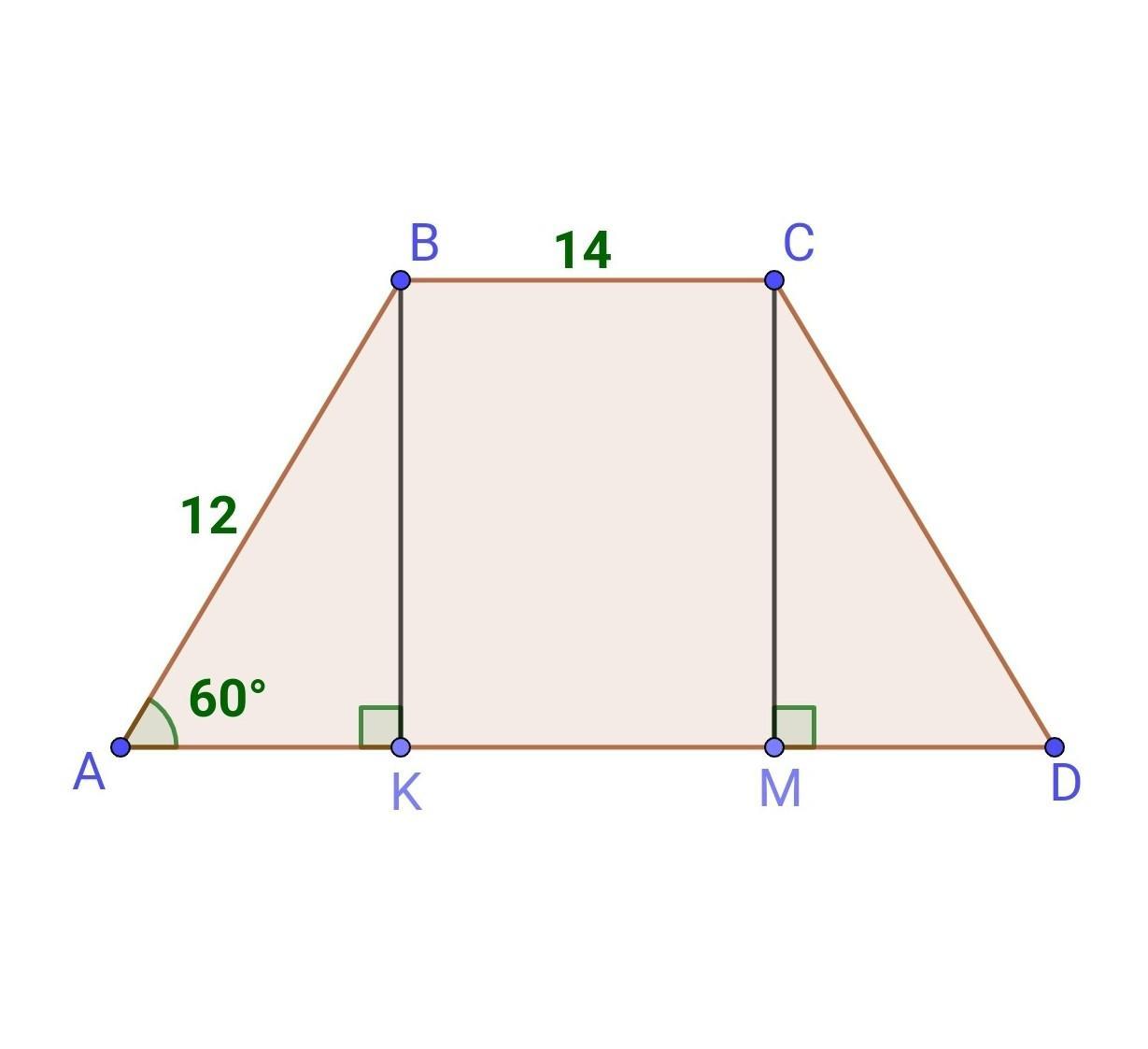
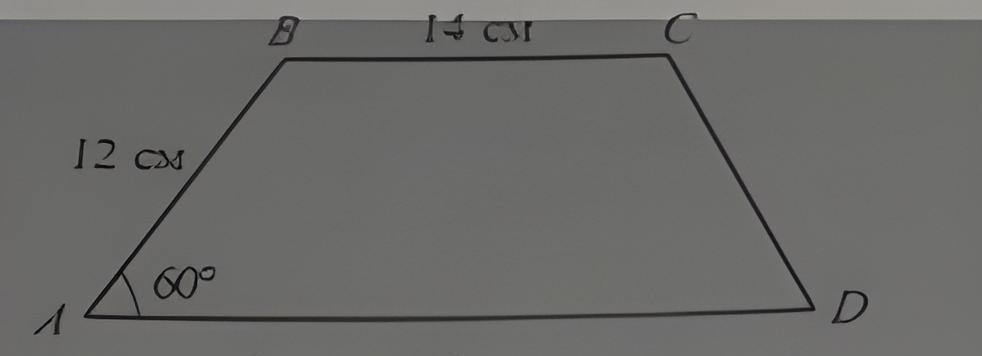
Используя данные рисунка, найдите периметр равнобокой трапеции АВСD.
помогите пожалуйста!!!!
Ответы
Ответ:
Периметр трапеции равен 64 см.
Объяснение:
ДАНО: ABCD - трапеция, BC||AD, AB=CD, BC=14см, АВ=12 см, ∠А=60°.
НАЙТИ: Р(ABCD)
РЕШЕНИЕ
1) CD = AB = 12 (см) - как боковые стороны равнобокой трапеции.
2) Проведём две высоты ВК и СМ.
Рассмотрим прямоугольный треугольник ABK(∠AKB=90°)
По свойству острых углов прямоугольного треугольника:
∠А+∠АВК=90°
∠АВК=90°-∠А=90°-60°=30°.
Тогда АК = ½ • АВ = ½ • 12 = 6 (см) - как катет, лежащий напротив угла 30°.
3) Рассмотрим △ABK и △DCM.
У них:
- ∠A=∠D - как углы при основании равнобедренной трапеции
- AB=CD - как боковые стороны равнобедренной трапеции
△ABK = △DCM (по гипотенузе и острому углу).
Значит АК = MD = 6 (см)
4) Поскольку KBCD - прямоугольник, то KM = BC = 14 (см) - как противоположные стороны прямоугольника.
Тогда AD = AK + KM + MD = 6 + 14 + 6 = 26 (см)
5) Найдём периметр трапеции, как сумму всех её сторон:
P(ABCD) = AB + BC + CD + AD = 12 + 14 + 12 + 26 = 64 (см)
ОТВЕТ: 64 см
#SPJ1