Допоможіть, будь ласка.
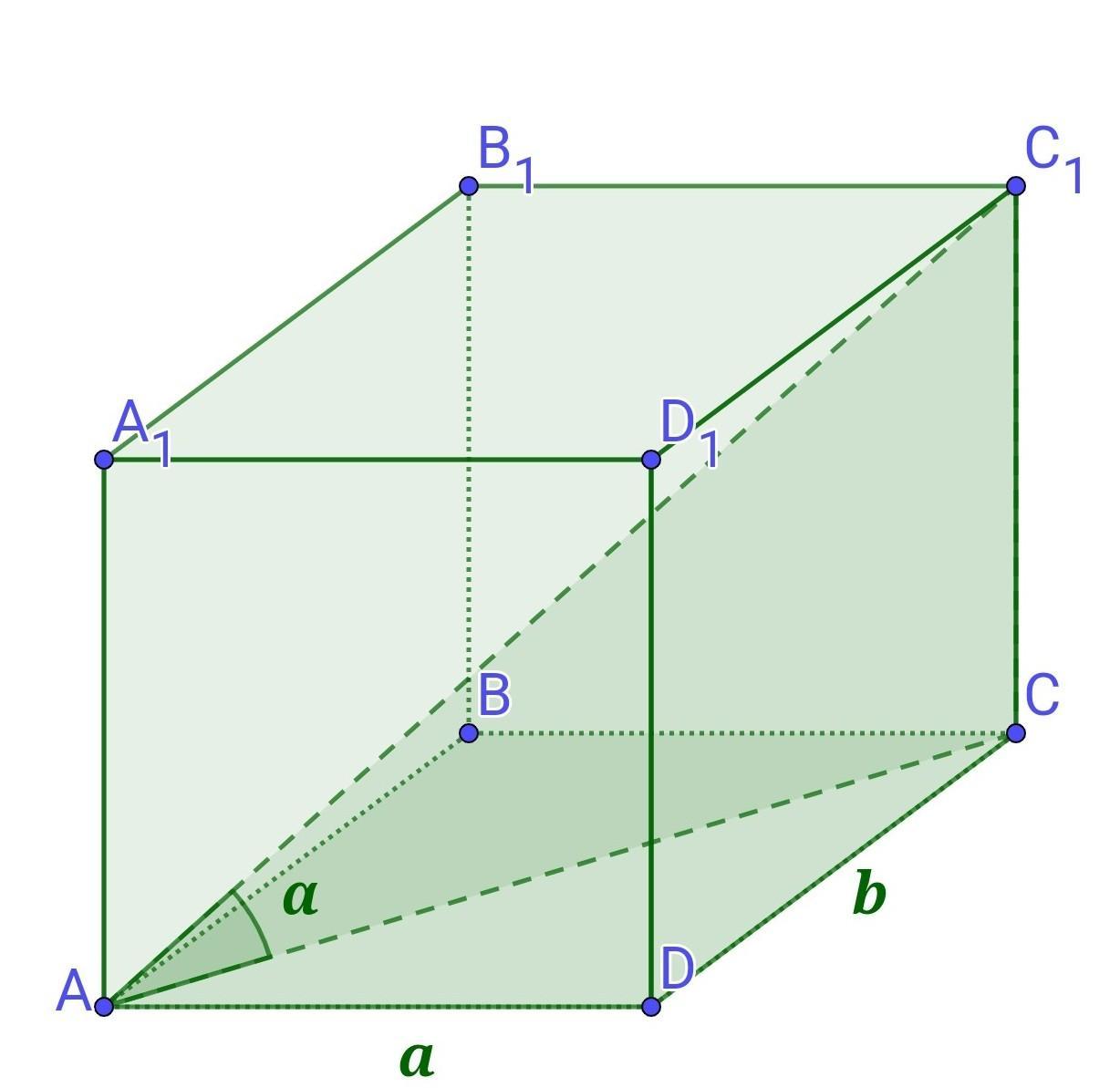
Знайти повну поверхню прямокутного паралелепіпеда, сторони основи якого дорівнюють a і b, а діагональ нахилена до площини основи під кутом α.
Найти полную поверхность прямоугольного параллелепипеда, стороны основания которого равны a и b, а диагональ наклонена к плоскости основания под углом α.
Ответы
Ответ:
Площа повної поверхні прямокутного паралелепіпеда дорівнює:
кв. од.
Объяснение:
Знайти повну поверхню прямокутного паралелепіпеда, сторони основи якого дорівнюють a і b, а діагональ нахилена до площини основи під кутом α.
Розв'язання
Кожна грань прямокутного паралелепіпеда є прямокутником.
У прямокутного паралелепіпеда бічне ребро (висота) перпендикулярне до площини основи (прямокутника ABCD), тому бічне ребро перпендикулярне до кожного відрізка, що лежить в площині основи, тобто CC₁⊥AC.
Так як CC₁⊥AC, то відрізок AC (діагональ квадрата) є ортогональною проекцією діагоналі призми AC₁, тому:
∠C₁AC=α – кут між діагоналлю призми і площиною основи і ΔC₁AC – прямокутний (∠ACC₁=90°).
1) З прямокутного трикутника ACD(∠D=90°), в якому AD = a, DC = b - катети, за теоремою Піфагора знайдемо гіпотенузу АС - діагональ основи паралелепіпеда:
AC²=AD²+DC²
AC²=a²+b²
2) Розглянемо прямокутний трикутник ACC₁(∠ACC₁=90°), в якому АС прилеглий катет до кута ∠С₁АС=α.
За означенням тангенса гострого кута прямокутного трикутника знайдемо бічне ребро СС₁ паралелепіпеда:
CC₁ = AC • tg α
3) Площа повної поверхні - сума площ всіх граней паралелепіпеда.
S(пов) = S(біч) + 2 • S(осн)
S(біч) = Р(осн) • Н, де Н = СС₁
P(осн) =2(AD +DC) = 2(a+b)
S(біч) =
S(осн) = AD•DC = ab
Отже, площа повної поверхні прямокутного паралелепіпеда становить:
кв. од.
#SPJ1