Question

ПОЖАЛУЙСТА ЗАДАЧА 2 ПОМОГИТЕ ОЧЕНЬ СРОЧНО

Answer 1

Я незнаю правильно їли нет

Answer 2

Ответ:

∠ABC = 133°, ∠BCD = 47°, ∠ADC = 47°, ∠BAD = 133°

Объяснение:

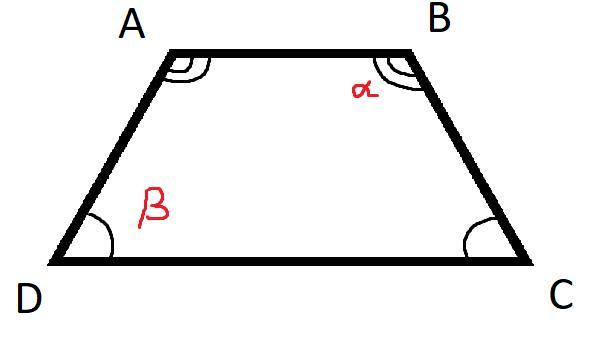
Дано: равнобедренная трапеция ABCD

разница противоположных углов трапеции равна 86°

Найти: ∠ABC, ∠BCD, ∠ADC, ∠BAD

Решение:

Пусть ∠ABC = α и ∠BCD = β, тогда так как трапеция ABCD - равнобедренная, углы при основании такой трапеции равны. Значит: ∠ABC = ∠BAD = α   и   ∠BCD = ∠ADC = β.

Основание АВ меньше основания DC, тогда α > β.

По условию задачи, разница противоположных углов трапеции равна 86°. Тогда:

α - β = 86°

α = (86 + β)°

Сумма всех углов четырехугольника равна 360°:

β + β + α + α = 360°

2β + 2α = 360°

2(β + α) = 360°

Так как α = (86 + β)°, то

2(β + 86 + β) = 360°

2β + 86 = 180°

2β = 94°

β = 47°

Так как α = (86 + β)°, то

α = (86 + 47)

α = 133°

Значит: ∠ABC = 133°, ∠BCD = 47°, ∠ADC = 47°, ∠BAD = 133°