ПОМОГИТЕ ДАЮ 100 балов!!!!
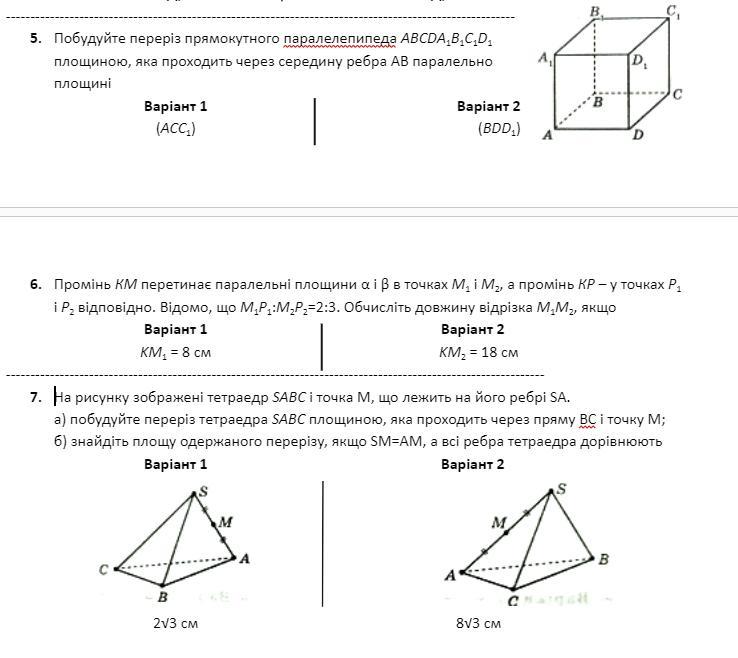
1)Побудуйте переріз прямокутного паралелепипеда ABCDA1B1C1D1 площиною, яка проходить через середину ребра АВ паралельно площині
Варіант 1
(ACC1)
2)Промінь КМ перетинає паралельні площини α і β в точках М1 і М2, а промінь КР – у точках Р1 і Р2 відповідно. Відомо, що М1Р1:М2Р2=2:3. Обчисліть довжину відрізка М1М2, якщо
Варіант 1
KM1 = 8 см
3)На рисунку зображені тетраедр SABC і точка М, що лежить на його ребрі SA.
а) побудуйте переріз тетраедра SABC площиною, яка проходить через пряму ВС і точку М;
б) знайдіть площу одержаного перерізу, якщо SM=AM, а всі ребра тетраедра дорівнюють
Варіант 1
Ответы
1.Для побудови перерізу прямокутного паралелепіпеда ABCDA1B1C1D1 площиною, яка проходить через середину ребра AB і паралельно площині ACC1, спочатку визначимо середину ребра AB, яку позначимо як M.
M буде точкою середини відрізка AB, тобто M = (A + B) / 2.
Далі, побудовуємо площину, паралельну площині ACC1 і проходячу через M. Ця площина буде перетинати паралелепіпед і отримаємо переріз.
2.Для обчислення довжини відрізка М1М2, можна використати пропорцію М1Р1:М2Р2 = 2:3. Якщо KM1 = 8 см, то:
M1Р1 / M2Р2 = 2 / 3.
Тобто, M1Р1 дорівнює 2/5 від відрізка KM1, і M2Р2 дорівнює 3/5 від відрізка KM1.
M1Р1 = (2/5) * 8 см = 16/5 см.
Тепер можемо знайти довжину відрізка M1М2:
M1М2 = M1Р1 + M2Р2 = (16/5 + 24/5) см = 40/5 см = 8 см.
Отже, довжина відрізка M1М2 дорівнює 8 см.
3.
Для побудови перерізу тетраедра SABC площиною, яка проходить через пряму ВС і точку М, спочатку визначимо точку перетину цієї площини з ребрами тетраедра.
a) Перетин прямої ВС з площиною, яка проходить через точку М, буде відрізком ВМ. Оскільки SM = AM, то точка М знаходиться посередині ребра SA, тобто М = (S + A) / 2.
Тепер, знаючи точку М, можна побудувати переріз тетраедра SABC.
б) Для знаходження площі отриманого перерізу, потрібно знати геометричні параметри тетраедра SABC. Однак в тексті відсутні значення всіх ребер та кутів, тому без цих відомостей не можливо точно знайти площу перерізу.
Ответ:
Відповідь на фотоооооо


