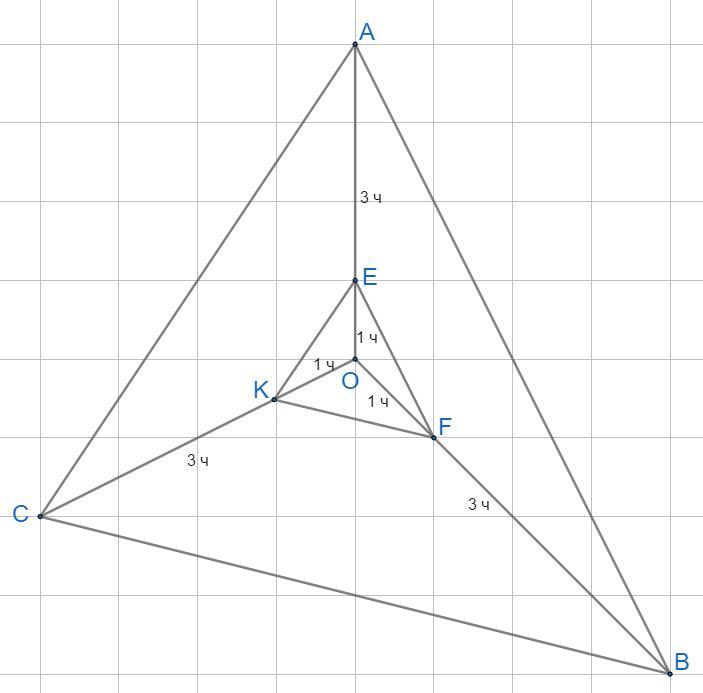
У внутрішній частині ΔABC взято довільну точку O. Точки E, F, K ділять відповідно відрізки OA, OB, OC у відношенні 1:3, починаючи від точки O. Знайдіть периметр ΔEFK (у см), якщо периметр ΔABC дорівнює 24 см.
Ответы
Ответ:
Периметр ΔEFK = 6 см.
Объяснение:
Во внутренней части ΔABC взята произвольная точка O. Точки E, F, K делят соответственно отрезки OA, OB, OC в отношении 1:3, начиная от точки O. Найдите периметр ΔEFK (в см), если периметр ΔABC равен 24 см.
Рисунок прилагается.
1) Рассмотрим треугольники KOE и COA.
По условию OE : EA = 1 : 3 и OK : KC = 1 : 3
Тогда OE : OA = 1 : 4 и OK : OC = 1 : 4,
то есть OE : OA = OK : OC = 1 : 4,
∠KOE = ∠COA - это общий угол в обоих треугольниках.
ΔKOE подобен ΔCOA по двум пропорциональным сторонам и углу между ними. Коэффициент подобия равен 1/4.
⇒ KE : CA = 1/4.
2) Аналогично ΔEOF подобен ΔAOB с коэффициентом подобия 1/4 по двум пропорциональным сторонам и углу между ними.
По условию OE : EA = 1 : 3 и OF : FB = 1 : 3;
Тогда OE : OA = OF : OB = 1 : 4,
∠EOF = ∠AOB - общий угол.
⇒ EF : AB = 1/4.
3) Аналогично ΔKOF подобен ΔCOB с коэффициентом подобия 1/4 по двум пропорциональным сторонам и углу между ними.
По условию OK : KC = 1 : 3 и OF : FB = 1 : 3;
Тогда OK : OC = OF : OB = 1 : 4,
∠KOF = ∠COB - общий угол.
⇒ KF : CB = 1/4.
4) ΔKEF подобен ΔABC по трем пропорциональным сторонам с коэффициентом подобия 1/4.
KE : CA = EF : AB = KF : CB = 1/4.
5) Коэффициент подобия подобных фигур равен отношению их соответствующих линейных размеров.
Тогда отношение периметров
P(ΔKEF) : P(ΔABC) = 1/4.
P(ΔKEF) = (1/4) · P(ΔABC) = (1/4) · 24 = 6 (см).
Периметр ΔKEF = 6 см.
#SPJ1