Question

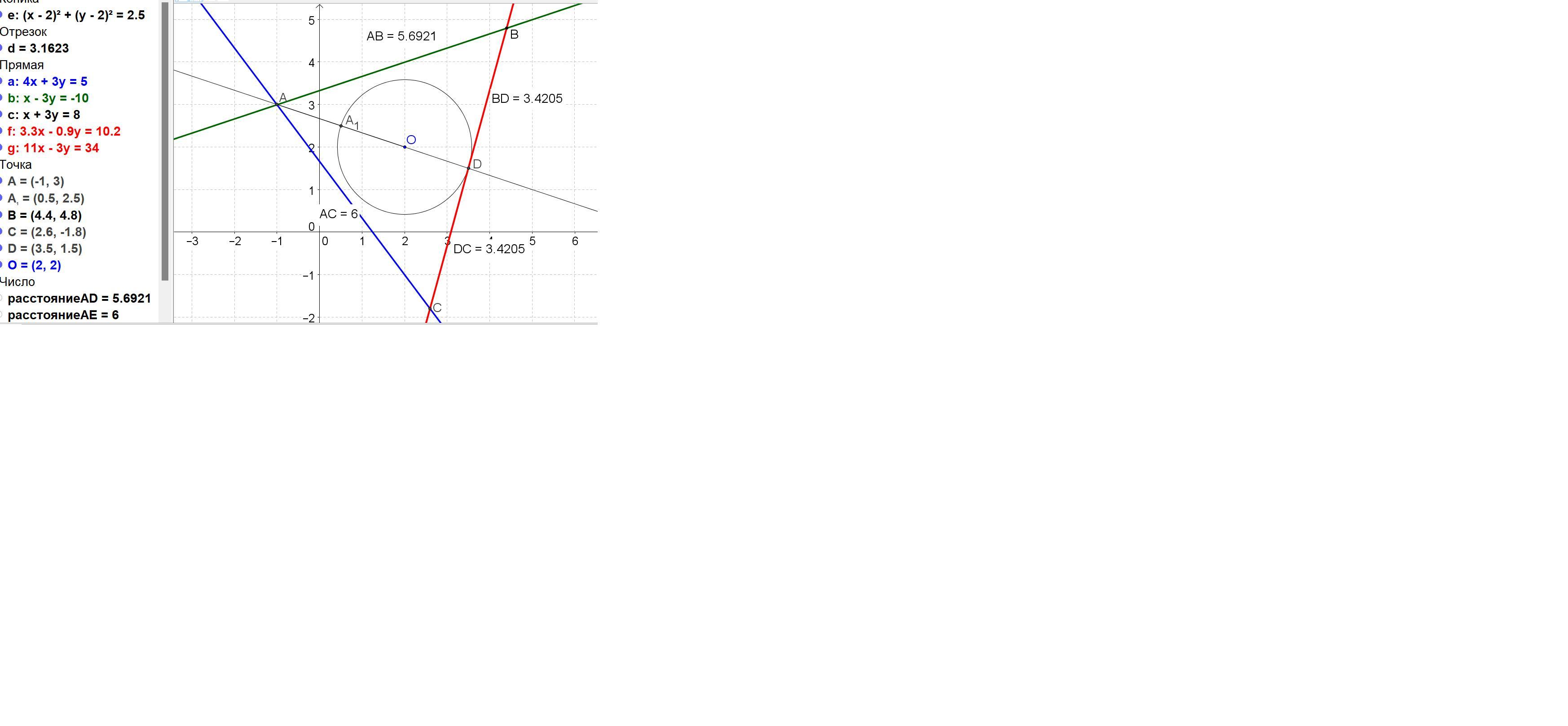
найдите 3 сторону треугольника пожалуйста, срочно

Answer 1

Ответ: 11x – 3y – 34 = 0.

Пошаговое объяснение:

Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1 , считая от вершины треугольника.

Находим координаты точки А как точки пересечения заданных прямых.

4x + 3y – 5 = 0,

x – 3y + 10 = 0   (+)

5x + 5 = 0,

x = -5/5 = -1.

y = (x + 10)/3 = (-1 + 10)/3 = 3.

Точка А(-1; 3).

Находим координаты точки А1, как середины отрезка АО:

х(А1) = (-1+2)/2 = 0,5.

у(А1) = (3+2)/2 = 2,5.  Точка А1(0,5; 2,5).

Теперь находим основание медианы (точка D) как точка, симметричная точке А1 относительно точки О.

x(D) = 2x(O) – xA1 = 2*2 – 0,5 = 3,5.

y(D) = 2y(O) – yA1 = 2*2 – 2,5 = 1,5. Точка D(3,5; 1,5).

A(x1,y1) - точка пересечения искомой прямой с прямой 4x + 3у – 5 = 0.

B(x2,y2)- - точка пересечения искомой прямой с прямой x – 3у + 10 = 0

D(3,5; 1,5) -  точка пересечения медианы с искомой прямой (середина отрезка)

Точка D(3,5; 1,5) принадлежит медиане.

Составляем систему

(x1+x2)/2=3,5,

(y1+y2)/2=1,5,

y1= kx1 + b1 = (1/3)x1+ (10/3),

y2= kx2 + b2 = (-4/3)x2 + (5/3)

Решаем систему.

x1+x2=7, x2 = 7 – x1.

y1+y2=3, y2 = 3 – y1.

Подставим в уравнения прямых.

3 – y1= (-4/3)(7 – x1) + (5/3),

-y1 = (-28/3) + (4/3)x1 + (5/3) – 3,

y1 = (28/3) - (4/3)x1 - (5/3) + 3,

y1 = -(4/3)x1 + (32/3). Заменим y1= (1/3)x1+ (10/3).

(1/3)x1+ (10/3) =  -(4/3)x1 + (32/3).

(5/3)х1 = (22/3), отсюда х1 = 22/5 = 4,4.

y1 = -(4/3)x1 + (32/3) = (-4/3)*(22/5) + (32/3) = (-88/15) + (160/15) = 72/15 = 4,8.

Найдены координаты точки В(4,4; 4,8).

Теперь по координатам точек В(4,4; 4,8) и D(3,5; 1,5)  находим уравнение третьей стороны.

(x – (22/5))/(3,5 – 4,4) = (y – (24/5))/(1,5 – 4,8),

(x – (22/5))/(-0,9) = (y – (24/5))/(–3,3),

(5x – 22)/(-4,5) = (5y – 24)/(-16,5),

-16,5*(5x – 22) = -4,5*(5y – 24),

(11/2))*(5x – 22) = (3/2)*(5y – 24),

55x – 242 = 15y – 72,

55x – 15y – 170 = 0,

11x – 3y – 34 = 0.

Получили общее уравнение третьей стороны.