Предмет: Алгебра,
автор: kirilldanilov251207
Решить не равенства используя метод интервалом.
Решить систему не равенства
Приложения:
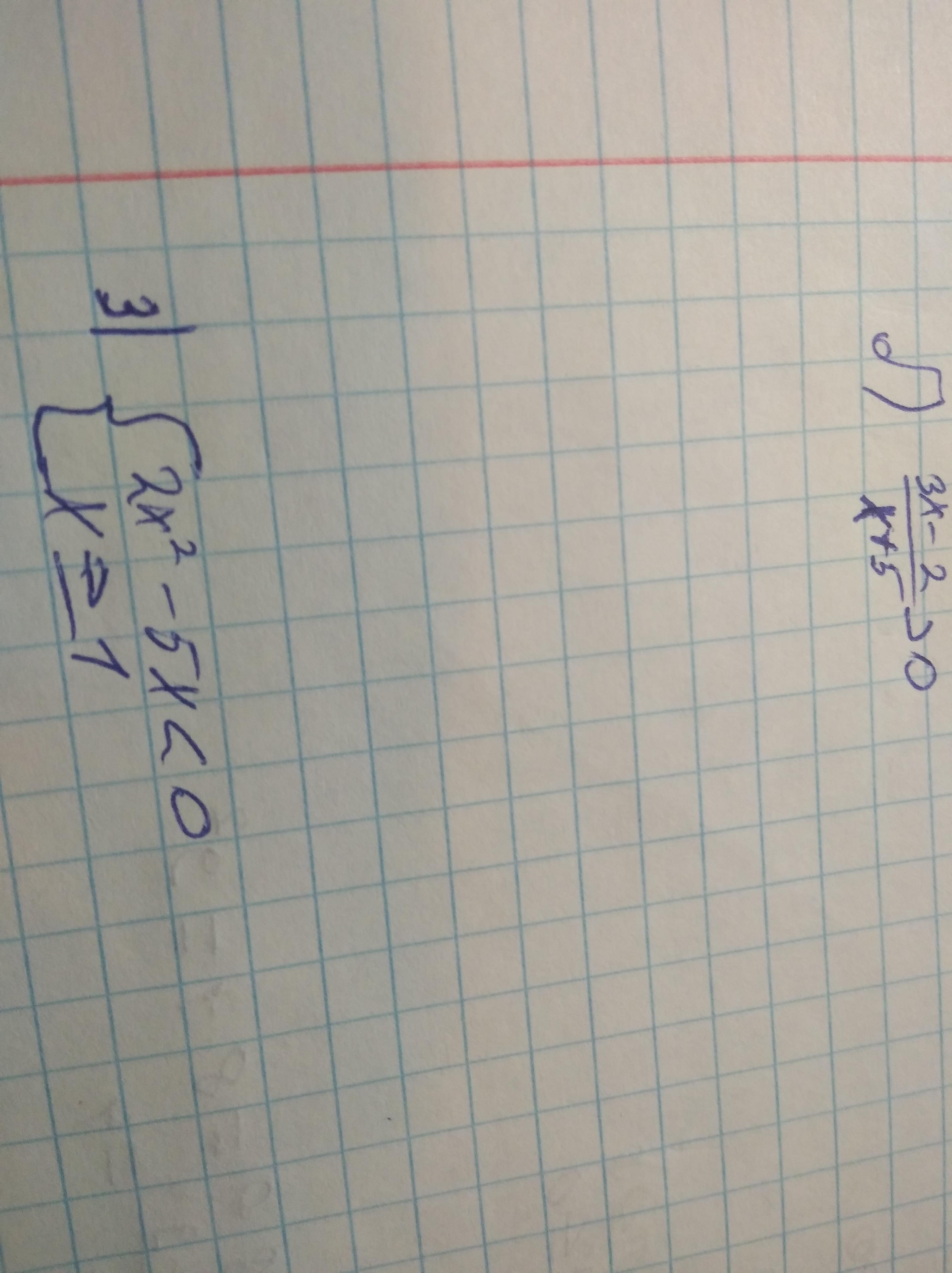
Ответы
Автор ответа:
2
Ответ:
1. х ∈ (-∞; -5) ∪ (2/3; +∞)
2. х ∈ [1; 5)
Объяснение:
1.
Применим метод интервалов.
Сначала домножим обе части неравенства на (х+5)
(3х-2)(х+5) > 0
Найдем корни двух уравнений
3х - 2 = 0 х₁ = 2/3
х + 5 = 0 х₂ = -5
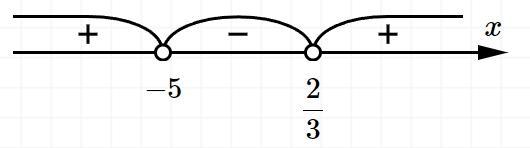
Наносим эти точки на числовую ость и смотрим, на каких интервалах выполняется неравенство
Например, на интервале (-∞: -5) возьмем число -(6) подставим его в неравенство. Получим
Аналогично проделаем на других интервалах и получим то, что изображено на рисунке.
Тогда наш ответ х ∈ (-∞; -5) ∪ (2/3; +∞)
2.
поэтому неравенство будет выполняться только при (x-5)< 0. ⇒ x < 5
получили решение для первого уравнения х < 5
и условие для второго уравнения х ≥ 1
Объединим эти решения и получим ответ
х ∈ [1; 5)
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: arinamanilenko
Предмет: География,
автор: sololiza11
Предмет: Физика,
автор: aliyevtofik35
Предмет: Биология,
автор: ujsumbaevaliappar