Предмет: Алгебра,
автор: onoprienkoliana
Розвʼяжіть нерівність, завдання на фото
Приложения:
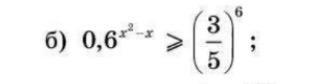
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Нули:
tamarabernukho:
...
Похожие вопросы
Предмет: Литература,
автор: sofiygrigoruk
Предмет: Литература,
автор: COJIHUIIIKO
Предмет: История,
автор: kiki209
Предмет: Геометрия,
автор: ssskafd
Предмет: Физкультура и спорт,
автор: 870059