Предмет: Геометрия,
автор: tamaesengoku
ДАЮ 90 БАЛЛОВ (СРОЧНО)
Приложения:
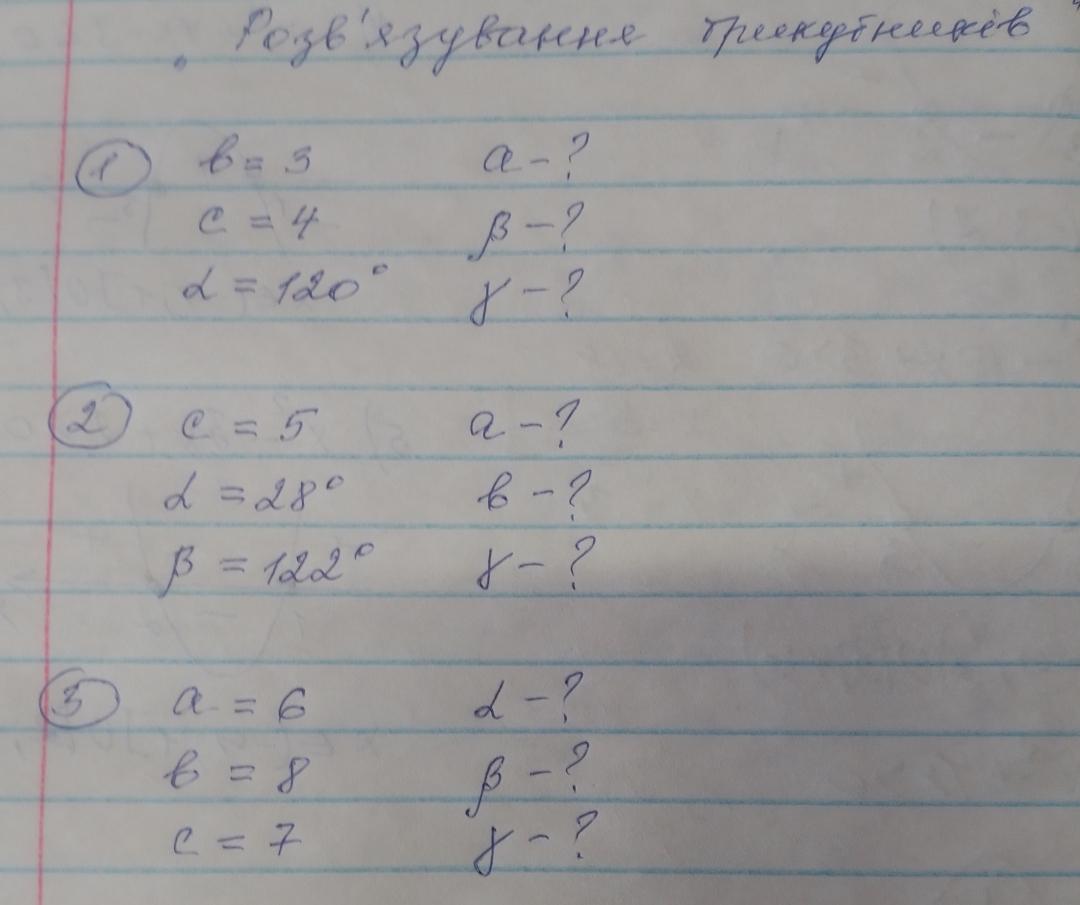
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1) по теореме косинусов:
для нахождения угла воспользуемся теоремой синусов;
третий угол найдем по теореме о внутренних углах треугольника:
ω=180°=> ω=180-(
=180°-(120°-25°)=180°-145°=35°
Здесь вместо угла гамма использовал угол ω так как нету здесь данного обозначения для угла гамма.
2) Cначала найдем третий угол из теоремы которая была использована выше: ω=180°=>ω=180°-(28°+122°)=180°-150°=30°
Для нахождения сторон a и b используем теорему синус:
3) Используем для нахождения угла теорему косинусов:
угол можно найти по теореме синусов:
и третий угол найдем из теоремы о внутренних углах треугольника:
ω=180°-(47°+77°)=180°=56°
Похожие вопросы
Предмет: Английский язык,
автор: rizavalievam
Предмет: Другие предметы,
автор: kabyd04
Предмет: Литература,
автор: dan3005poc
Предмет: Литература,
автор: daurbekov031
Предмет: Другие предметы,
автор: Asya294739220