СРОЧНО!!!
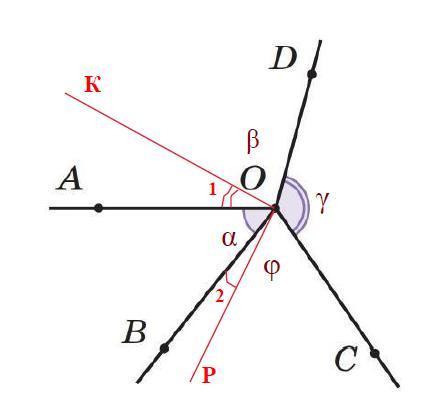
Из точки О в указанном порядке выходят лучи ОА, ОВ, ОС и OD. Известно, что сумма углов AОB и COD равна 180°. Какой угол образуют биссектрисы углов АОС и BOD?

Ответы
Ответ:
Объяснение:
1) Введем следующие обозначения:
∠АОВ = α; ∠АОD = β; ∠DОС = γ; ∠BOC = φ
2) α+γ = 180° по условию. Т.к. сумма всех углов = 360°, то и
β + φ =180°
3) ∠ВОD = ∠АОВ + ∠АОD = α + β
Т.к. КО - биссектриса ∠ВOD, то
∠ВОК = (α + β)/2 В то же время
∠ВОК = α + ∠1. Составим уравнение:
(α + β)/2 = α + ∠1
α + β = 2(α + ∠1) → α + β - 2α = 2*∠1 → β - α = 2*∠1
4) ∠АОС = α + φ, т.к. ОР - биссектриса ∠АОС, то
∠АОР = (α + φ)/2, но ∠АОР = α +∠2. Составим уравнение:
(α + φ)/2 = α +∠2 → α + φ = 2(α +∠2) → φ - α = 2*∠2
5) Составим систему:
{β - α = 2 *∠1
+ {φ - α = 2*∠2
------------------------------
β - α + φ - α = 2*∠1 + 2*∠2 Но т.к. β + φ =180°, значит
180° -2α = 2(∠1 + ∠2)
180° = 2(∠1 + ∠2) + 2α
∠1 + ∠2 + α = 180°/2
∠1 + ∠2 + α = 90° или
∠1 + ∠2 + ∠АОВ = 90°
Но (∠1 + ∠2 + ∠АОВ) = ∠КОР - угол между биссектрисами углов АОС и BOD.
Ответ: биссектрисы углов АОС и BOD образуют прямой угол.