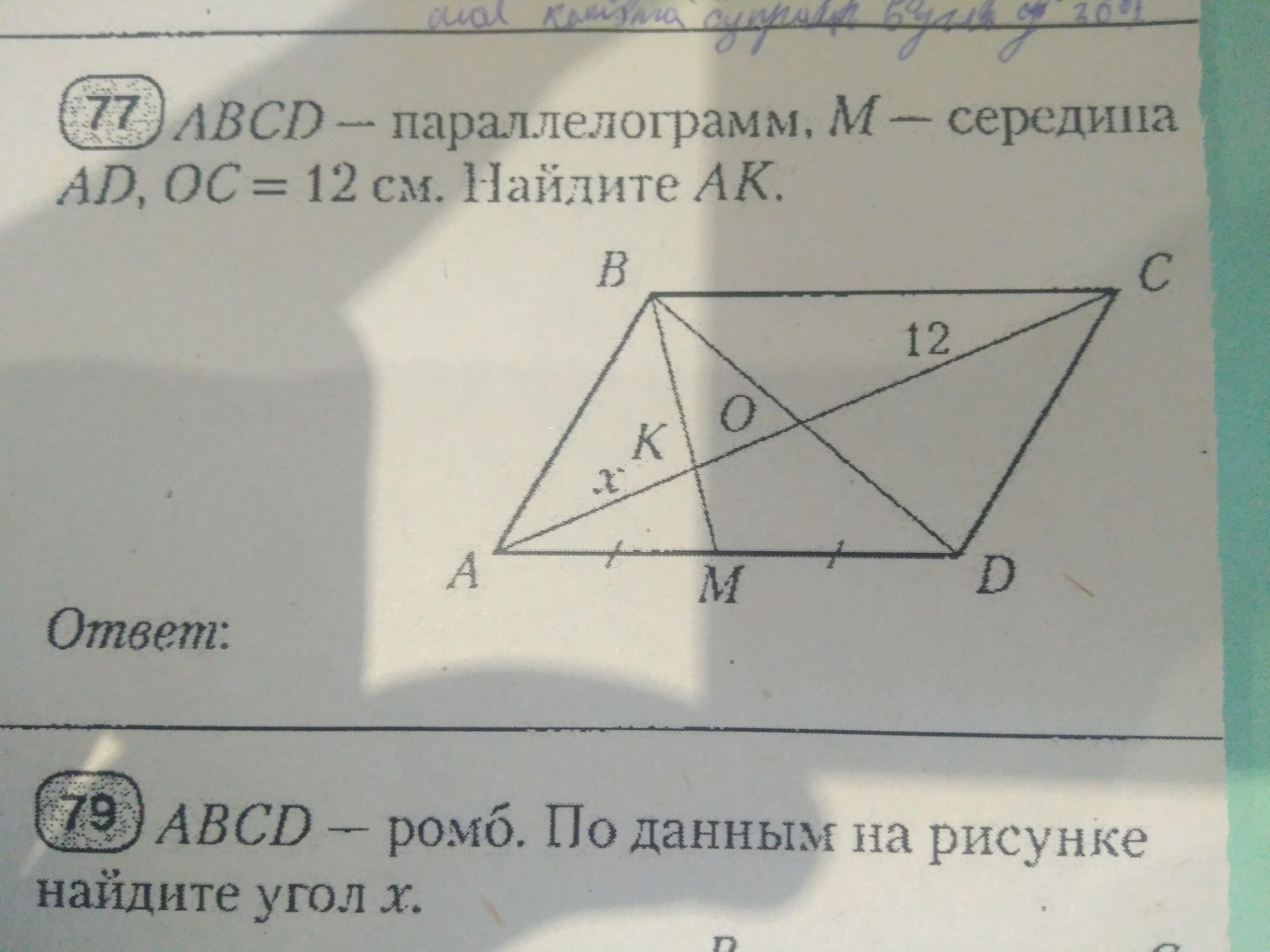
ABCD–параллелограмм,M–середина AD,OC=12см.Найдите AK.
Ответы
Ответ:
Для решения данной задачи необходимо использовать теорему о средней линии треугольника.
Теорема: средняя линия треугольника параллельна основанию и равна его половине.
Поскольку M - середина AD, то MK является средней линией треугольника ABD. Следовательно, MK || AB и MK = 1/2 AB.
Для нахождения AK необходимо найти отношение AK к MK.
Треугольники AKD и AOC подобны по двум углам (угол A - общий, угол ADK = углу ACO как соответственные углы при параллельных прямых). Из подобия треугольников следует пропорциональность соответствующих сторон:
AD/AO = AK/AO
AK = AD * OK / OA
Но OK = 12 (по условию), а OA = 2 OK (т.к. MK = 1/2 AB, а AB = 2 OK). Подставляя значения в формулу, получим:
AK = AD * 12 / 2 * 12 = AD / 2
Поскольку ABCD - параллелограмм, то AD = AB. Тогда:
AK = AB / 2 = MK
Ответ: AK = MK = 12 см.