как это решить ??? СРОЧНО
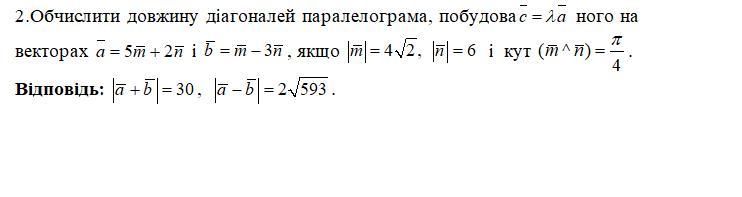
Ответы
Находим длину вектора а по теореме косинусов.
L(а) =√(5*|m|)² + (2*|n|)² - 2*|5m|*|2n|*cos(π – ( π /4))) =
= √((5*4√2)² + (2*6)² - 2*5*(4√2)*2*6*(-√2/2)) =
= √(800 + 144 + 480) = √1424 = 4√89 ≈ 37,793592.
Находим угол α между осью Ох и вектором (а).
cos α = (5*|m|)² + (L(а))² - (2*|n|)²)/(2*(5*|m|)*L(а)) =
= (800 + 1424 – 144)/(2*(20√2)*( 4√89)) = 2080/(160√178) = 13/(√178) =
≈ 0,974391.
α = arccos(13/(√178)) ≈ 0,226799 радиан или 12,99462 градуса.
L(b) =√(|m|)² + (-3*|n|)² - 2*|m|*|-3n|*cos(π/4)) =
= √((4√2)² + (3*6)² - 2*(4√2)*3*6*(√2/2)) =
= √(32 + 324 - 144) = √212 = 2√53 ≈ 14,56022.
Находим угол β между осью Ох и вектором (b).
Для этого сначала определим угол β1 между вектором (-3n) и вектором (b).
cos β1 = (3*|n|)² + (L(b))² - (|m|)²)/(2*(3*|n|)*L(b)) =
= (18² + 212 - (4√2)²)/(2*18*2√53) =
= (324 + 2124 – 32)/(2*18)*( 4√2)) = 504/(144√2) = 63/(18√2) =
≈ 0,961524.
β1 = arccos(63/(18√2)) ≈ 0,2783 радиан или 15,9454 градуса.
Так как угол вектора (-3n) равен -135 градусов, то угол равен:
β = -135 + 15,9454 = -119,0546.
Получаем угол между векторами a_b = 12,99462 – (-119,0546) = 132,04922 градуса.
Теперь находим сумму векторов a и b.
Но сначала надо найти угол γ между векторами.
γ = β1 + (π/4) – α = 15,9454 + 45 - 12,99462 = 47,95078 градуса.
L(a+b) = √((4√89)² + (2√53)² - 2*(4√89)*2√53)cos47,95078°) =
= √(1424 + 212 – 736) = √900 = 30 ед.
L(a-b) = √((4√89)² + (2√53)² - 2*(4√89)*2√53)cos(180 - 47,95078°) =
= √(1424 + 212 + 736) = √2372 = 48,70318 ед.
