Предмет: Алгебра,
автор: evikkovalchuk10
Помогите пожалуйста с заданиями во вложении.
(желательно объяснить на листке бумаги, чтобы было понятнее)
Приложения:
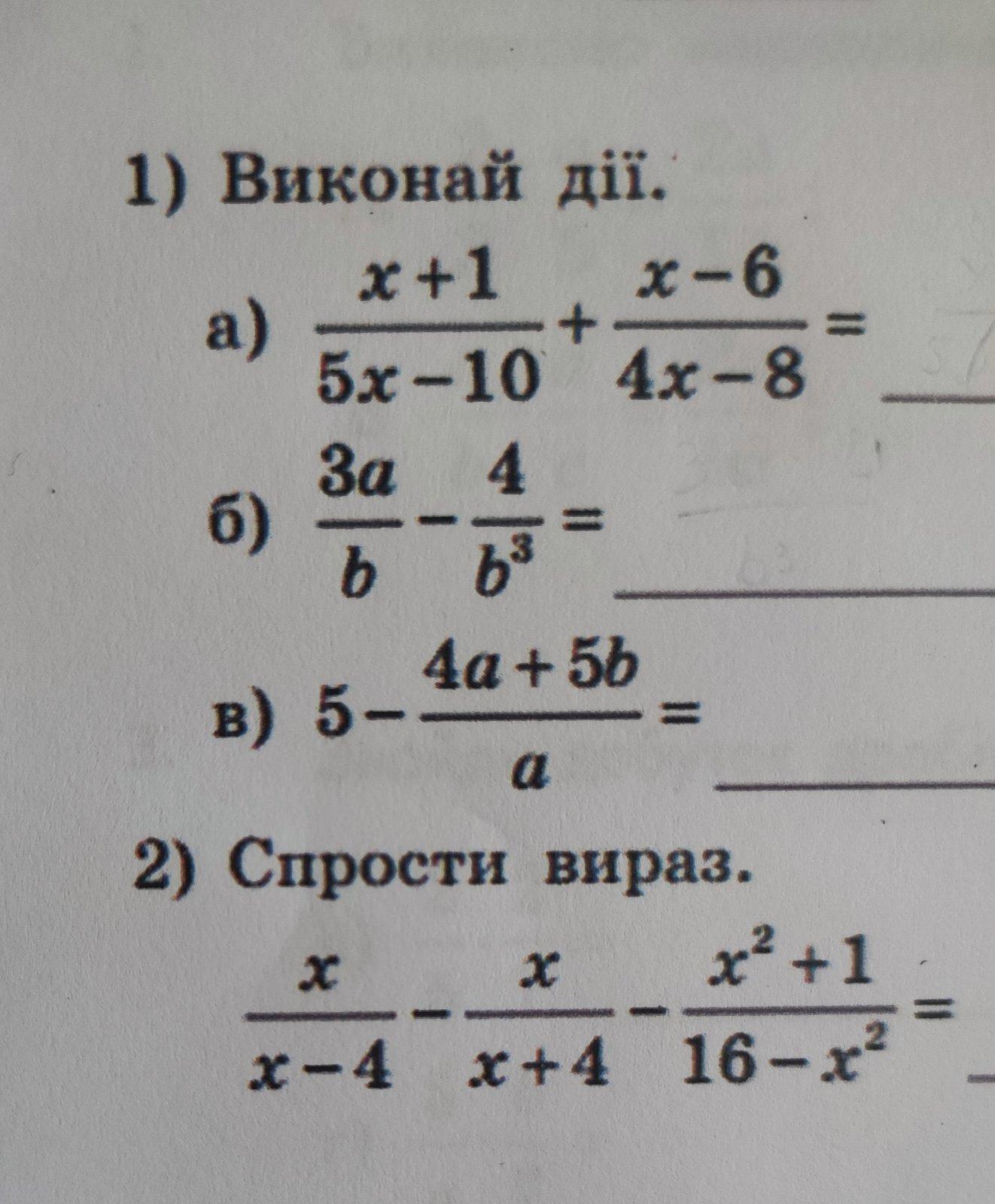
Ответы
Автор ответа:
1
Ответ:
1).
а)
б)
в)
2).
Похожие вопросы
Предмет: Английский язык,
автор: dobribratock
Предмет: Математика,
автор: danilmironov344
Предмет: Другие предметы,
автор: polisukvlada166
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: zhaba88