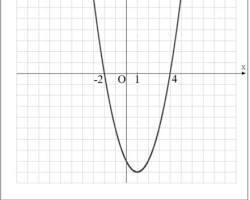
9.Решите неравенство: 2x² - 8 > 0
Ответы
Ответ:
Для решения данного неравенства сначала найдем корни квадратного уравнения, которое получается при приравнивании выражения \(2x^2 - 8\) к нулю:
\[2x^2 - 8 = 0\]
Разделим обе стороны на 2:
\[x^2 - 4 = 0\]
Решим квадратное уравнение:
\[x^2 = 4\]
\[x = \pm 2\]
Таким образом, корни уравнения \(2x^2 - 8 = 0\) равны \(x = -2\) и \(x = 2\).
Теперь проведем анализ неравенства \(2x^2 - 8 > 0\) относительно этих корней. Нам нужно определить, при каких значениях \(x\) выражение \(2x^2 - 8\) положительно.
1. Когда \(x < -2\), выражение \(2x^2 - 8\) положительно.
2. Когда \(-2 < x < 2\), выражение \(2x^2 - 8\) отрицательно.
3. Когда \(x > 2\), выражение \(2x^2 - 8\) снова положительно.
Таким образом, неравенство \(2x^2 - 8 > 0\) выполняется при \(x < -2\) и \(x > 2\).
Ответ:
Объяснение:
x² - 4 > 0
x² > 4
|x| > 2
x < -2 или x > 2