Question

1. Доведи, що бісектриси кутів паралелограма, які прилягають до однієї зі сторін, перетинаються під кутом 90°.
пожалуйста срочно! даю 40 балов
​

Answer 1

Відповідь:

Пояснення:

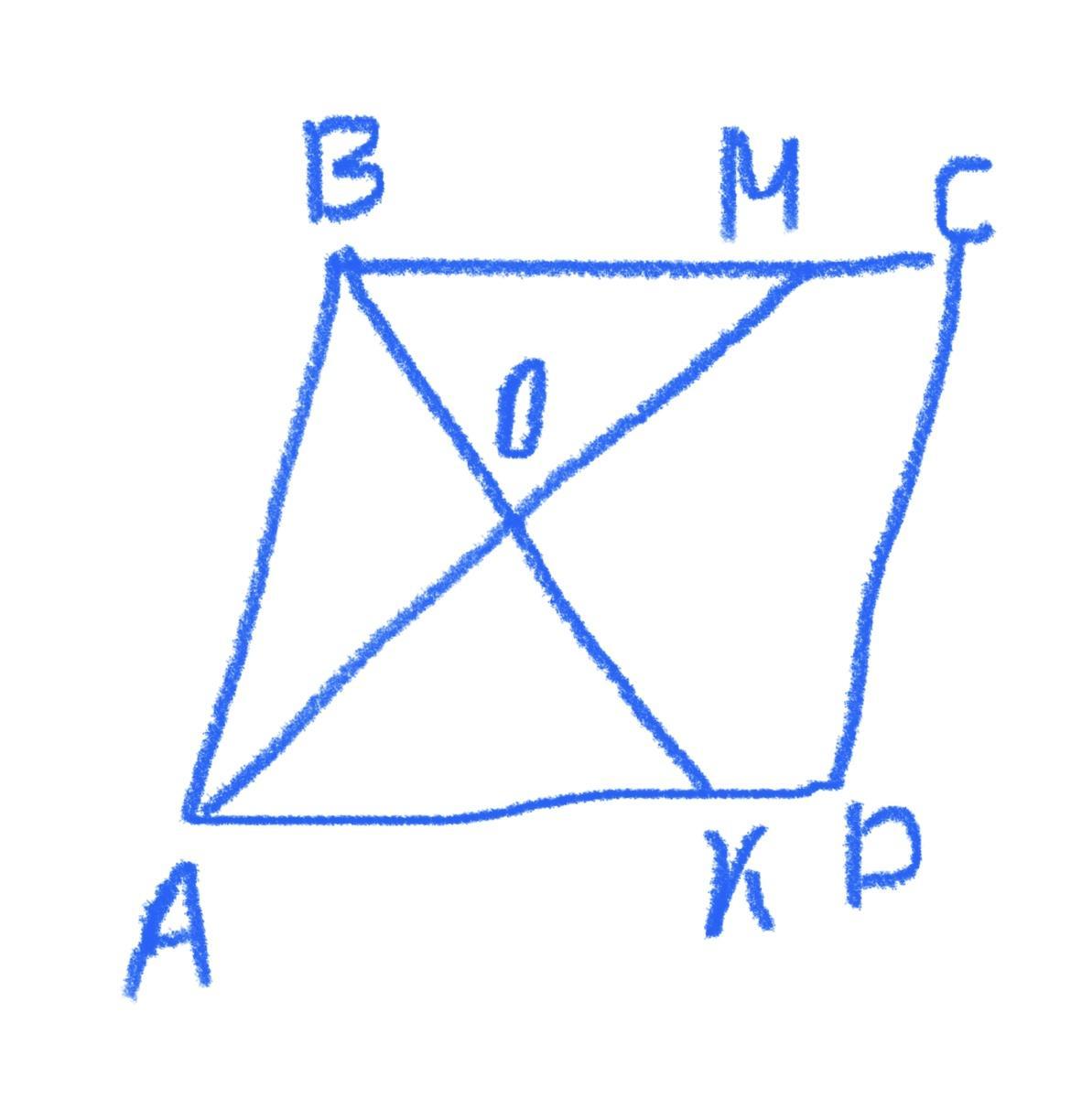
Дано:

АВСD - паралелограм;

АМ - бісектриса ∠А;

ВК - бісектриса ∠В.

Довести: АМ⊥ ВК

Доведення:

У паралелограма сума кутів, прилеглих до однієї сторони дорівнює 180*:

∠А + ∠В = 180*

Бісектриса кута ділить кут навпіл.

Точка О - точка перетину бісектрис АМ і ВК.

Розглянемо трикутник АОВ:

∠ВАО = 1/2•∠А

∠АВО = 1/2•∠В

∠ВАО + ∠АВО = 1/2•∠А + 1/2•∠В =

= 1/2•(∠А + ∠В) = 1/2•180 = 90*;

Сума кутів трикутника становить 180*.

∠АОВ = 180 - (∠ВАО + ∠АВО) = 180-

- 90= 90*
АМ⊥ ВК.

Отже. бісектриси кутів паралелограма, які прилягають до однієї зі сторін, перетинаються під кутом 90°.
Доведено.