Найдите область допустимых значений
y=x-x2 (x-x2 под корнем ) 100 баллов
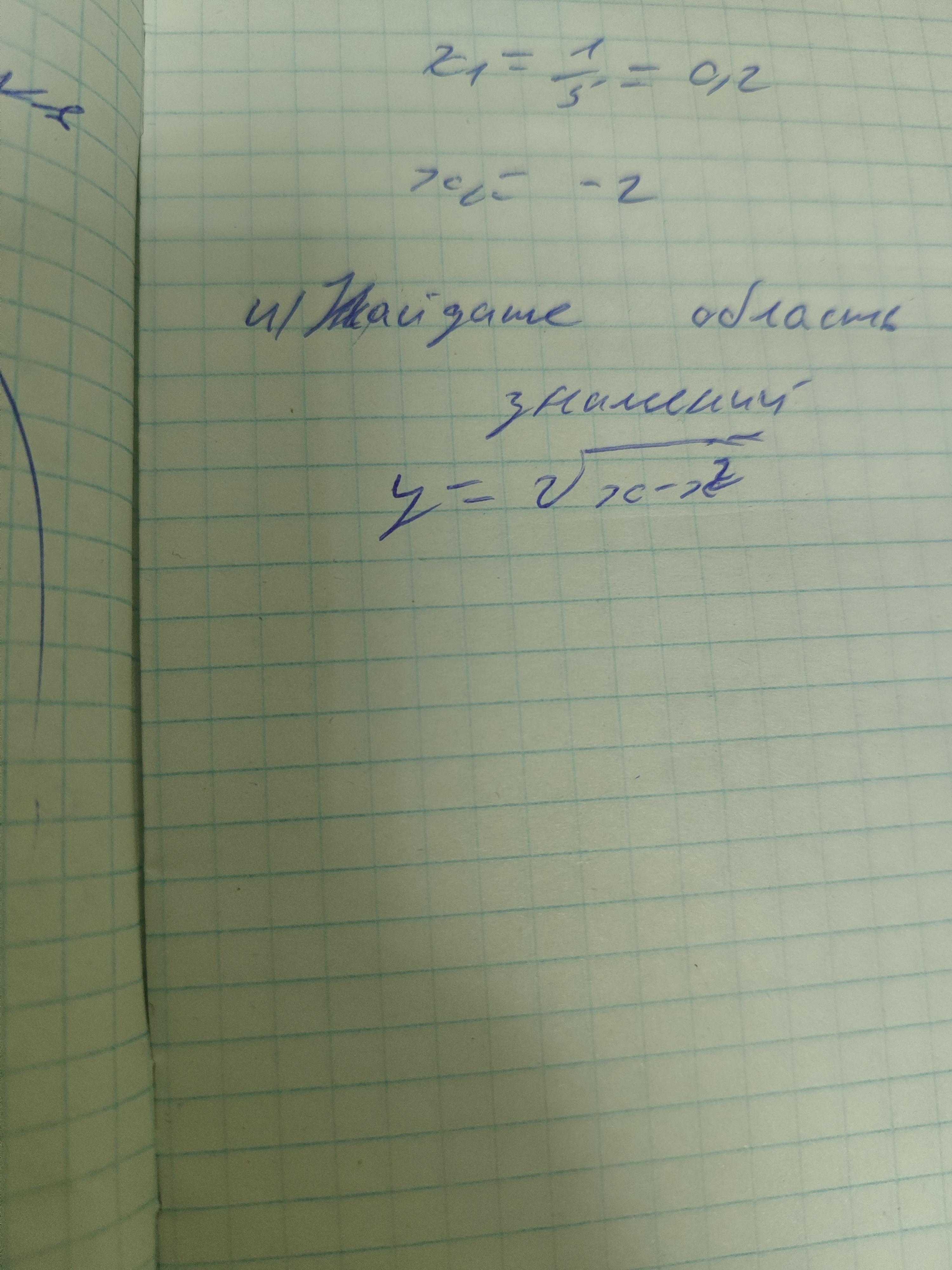
Ответы
Пошаговое объяснение:
Для нахождения области допустимых значений выражения y = x - x * sqrt(x - x^2), мы должны учесть, что значение под корнем (x - x^2) не может быть отрицательным, иначе получится комплексное число.
x - x^2 должно быть больше или равно нулю: x - x^2 >= 0.
Решим это неравенство: x(1 - x) >= 0.
Найдем корни уравнения x(1 - x) = 0. Эти точки делят область на интервалы, где неравенство выполняется и не выполняется.
Корни уравнения x(1 - x) = 0 равны x = 0 и x = 1.
Теперь мы можем определить область допустимых значений:
Если x < 0 или 0 < x < 1, то x(1 - x) > 0, и неравенство выполняется.
Если x = 0 или 1, то x(1 - x) = 0, и неравенство выполняется.
Если x > 1, то x(1 - x) < 0, и неравенство не выполняется.
Итак, область допустимых значений для данного выражения: x ∈ [0, 1] (включая 0 и 1)