Question

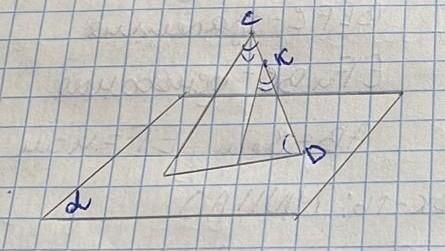
Точка К лежит на отрезке CD. CD пересекается с плоскольстью (альфа) в точке D. Через точки C и K проведены паралельные прямые пересекающие плоскость (альфа) к точках M и E . Найдите длину отрезка CD, если CM:KE , как 4:6 CK=3см​

Answer 1

Ответ:

Для решения данной задачи нам необходимо выполнить следующие действия:

1. Обозначим коэффициент пропорциональности через x. Тогда CM = 4x, KE = 6x.

2. Рассмотрим треугольники CKM и CKE. Они подобны по двум углам (вертикальные и накрест лежащие при параллельных прямых CK и KE и секущей CE).

3. Из подобия треугольников следует пропорциональность соответствующих сторон: CM/KE = CK/CE. Подставим значения сторон и выразим CE: 4x/6x = 3 - 4x / CE, (4x)/(6x) = (3 - 4x)/CE, 24x = 18x - 24x^2, 24x^2 + 6x - 18 = 0.

4. Решив квадратное уравнение, найдем x: x1 = (√(4 + 48))/12 = (√52)/12, x2 = (-√(4 + 48))/12 = -(√52)/12. Второй корень не подходит, так как x должен быть положительным числом.