Предмет: Математика,
автор: sosiso4ka195
СРОЧНО Знайти sina, якщо cos(a) = 3/7 < а < 2π
Приложения:
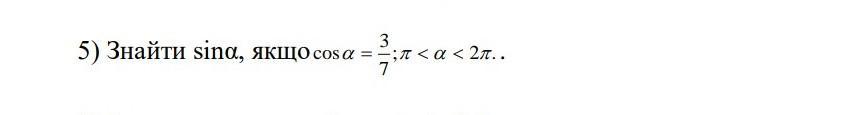
Ответы
Автор ответа:
1
Ответ:
Ниже.
Пошаговое объяснение:
Зная значение cos(a), мы можем найти значение sin(a) с помощью тождества sin^2(a) + cos^2(a) = 1.
Если cos(a) = 3/7, то cos^2(a) = (3/7)^2 = 9/49.
Тогда sin^2(a) = 1 - cos^2(a) = 1 - 9/49 = 40/49.
Так как sin(a) может быть как положительным, так и отрицательным, мы получаем два возможных значения: sin(a) = ±√(40/49) = ± 4√(10)/7.
Однако, поскольку задано, что π < a < 2π, то a находится в третьей или четвертой четверти координатной плоскости, где значение sin(a) отрицательно.
Таким образом, sin(a) = -4√(10)/7.
Похожие вопросы
Предмет: Математика,
автор: romanrassohin50m
Предмет: Другие предметы,
автор: evik28061984
Предмет: Химия,
автор: Аноним
Предмет: Русский язык,
автор: Udita
Предмет: Биология,
автор: nemetildeev2006