Предмет: Алгебра,
автор: Ononimys12
7. Упростите выражение: VX x-y ( - , x >0, y >0, x≠ y. x²+xy √x - √ √x + √
Приложения:
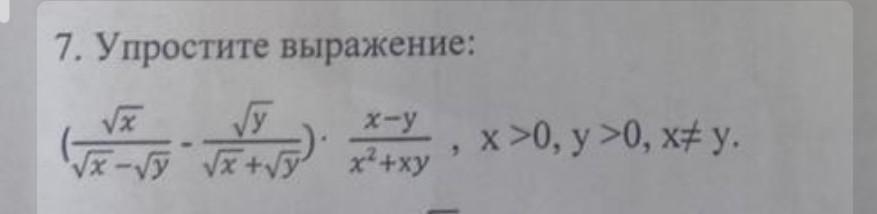
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: alexandraplatonova26
Предмет: Физика,
автор: HelloKing
Предмет: Другие предметы,
автор: alexandraplatonova26
Предмет: История,
автор: mmaarrss
Предмет: Литература,
автор: gostarina784