Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Продиференціювати функції.
Знайти похідну ....... та .......
Продифференцировать функции.
Найти производную ....... и .......
Приложения:
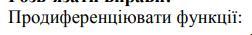
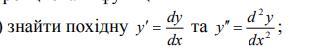
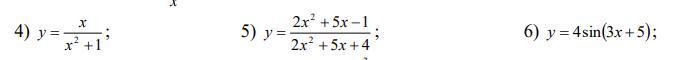
Ответы
Автор ответа:
1
------------------------------------------------------------------
------------------------------------------------------------------
fctdgsygfdhngfxzgsac:
дуже дякую)
Похожие вопросы
Предмет: Алгебра,
автор: kiril210
Предмет: Геометрия,
автор: alex6565
Предмет: Қазақ тiлi,
автор: elfbarmma
Предмет: Английский язык,
автор: dasdasaasas
Предмет: Математика,
автор: debilovicdebil741