Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовностей.
Приложения:
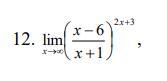

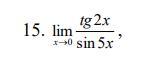
Ответы
Автор ответа:
1
Ответ:
в объяснении
Объяснение:
В 12) и 12) используем второй замечательный предел
12)
Выражение в скобках поделим числительна знаменатель и потом приведем всё ко второму замечательному пределу.
13) аналогично
3) первый замечательный предел
fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Биология,
автор: dahackasvatun
Предмет: Українська література,
автор: evaleshenko12
Предмет: Химия,
автор: vitalinagerasko1206
Предмет: Биология,
автор: bolatbekzanerke371
Предмет: Английский язык,
автор: kirillhabibullin06