Предмет: Алгебра,
автор: natalyabryukhova
Помогите решить неравенство
Приложения:
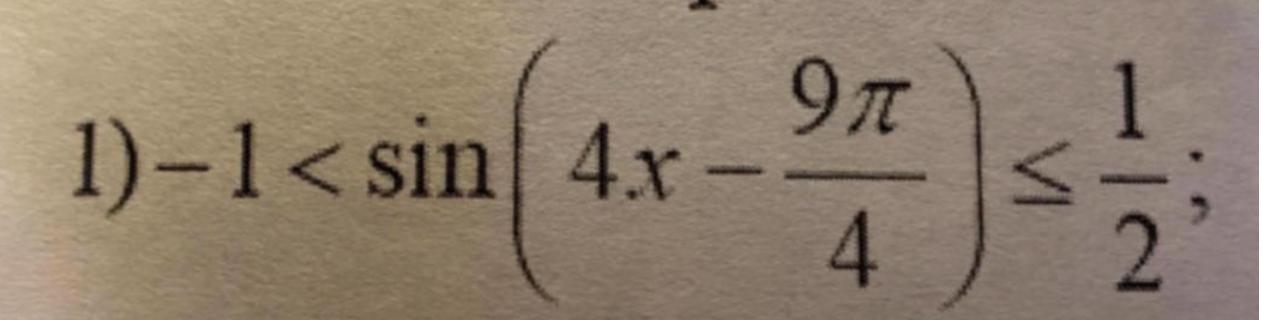
Ответы
Автор ответа:
3
Ответ:
Решить неравенство .
Если заменить аргумент на новую переменную t , то получим
Неравенство (*) равносильно системе неравенств
а) Решаем неравенство .
Так как для любых действительных значений t , то неравенство sin t > -1 верно при
.
б) Решаем неравенство ⇒
.
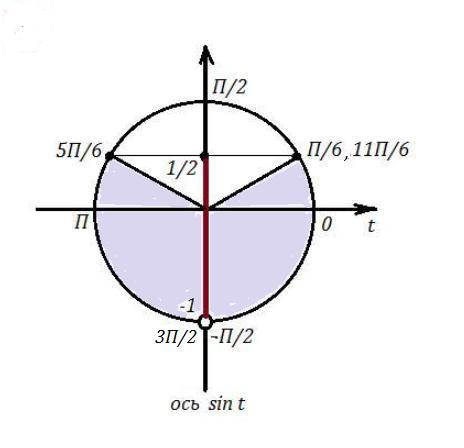
в) Теперь найдём пересечение множеств из пунктов а) и б) .
Учтём, что нужно из промежутка пункта б) выколоть точку
Тогда надо решить два неравенства .
и
.
Решаем неравенство , заменив переменную t на выражение , записанное через х .
Теперь решаем неравенство .
Объединив множества, получим ответ:
.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: tatianatipikina
Предмет: География,
автор: ze240946
Предмет: История,
автор: kochmaralisa
Предмет: Химия,
автор: Hannaoo
Предмет: Математика,
автор: Аноним