Question

фигура ограничена линиями y=1+x^3, y=0, x=-1, x=0 Вычислите: a)площадь фигуры ограниченной заданными линиями b)объем тела, образованного вращением круга оси Ox фигуры, ограниченной заданными линиями
помогите срочно пожалуйста

Answer 1

Ответ:

Объяснение:

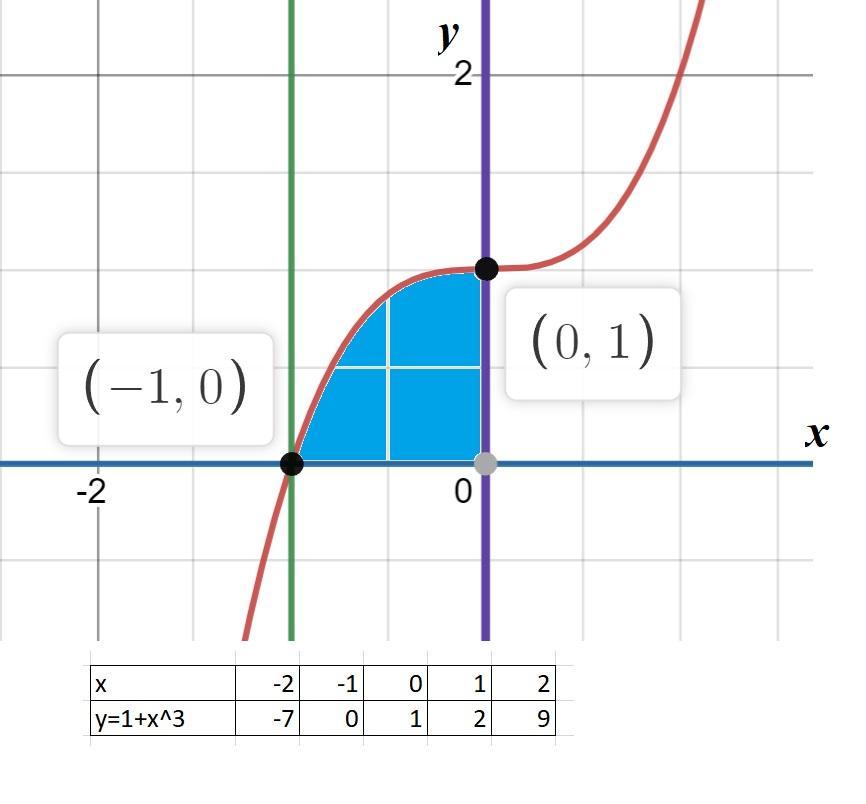
1) Строим графики функций  

y=1+x^3; y=0; x=-1; x=0 .  (См. скриншот)

a) Площадь  S=∫(a'b)f(x)dx.

Пределы интегрирования a=-1;  b=0.

f(x) = 1+x^3.  Тогда

S=∫(-1;0)(1+x^3)dx = ∫(-1;0)1dx +∫(-1;0)(x^3)dx = 1*x|(-1;0)+1/4 *x^4|(-1;0) =

= 1*(0-(-1)) + 1/4((0)^4-(-1)^4) = (0+1) + 1/4(0-1) = 1-1/4 = 3/4 кв. ед.

*************************

б)  Объем  V=π∫(a;b)f²dx.       вращение вокруг оси Ох

Пределы интегрирования a=0; b=1.

f(x) = 1+x^3. Тогда

V = π∫(0;1)(1+x^3)²dx = π∫(0;1)(1+2x^3+x^6)dx =

=  π(∫(0;1)1dx + 2∫(0;1)(x^3)dx + ∫(0;1)(x^6)dx)=

= π (x|(0;1) +2/4 (x^4)|(0.1) + 1/7(x^7)|(0;1) )=

= π (1-0) +1/2(1^4-0^4 + 1/7(1^7-0^7))   = π(1+1/2+1/7) = 23/14 π куб. ед.