Предмет: Алгебра,
автор: seva966
Помогите решить систему уравнения)))
Приложения:
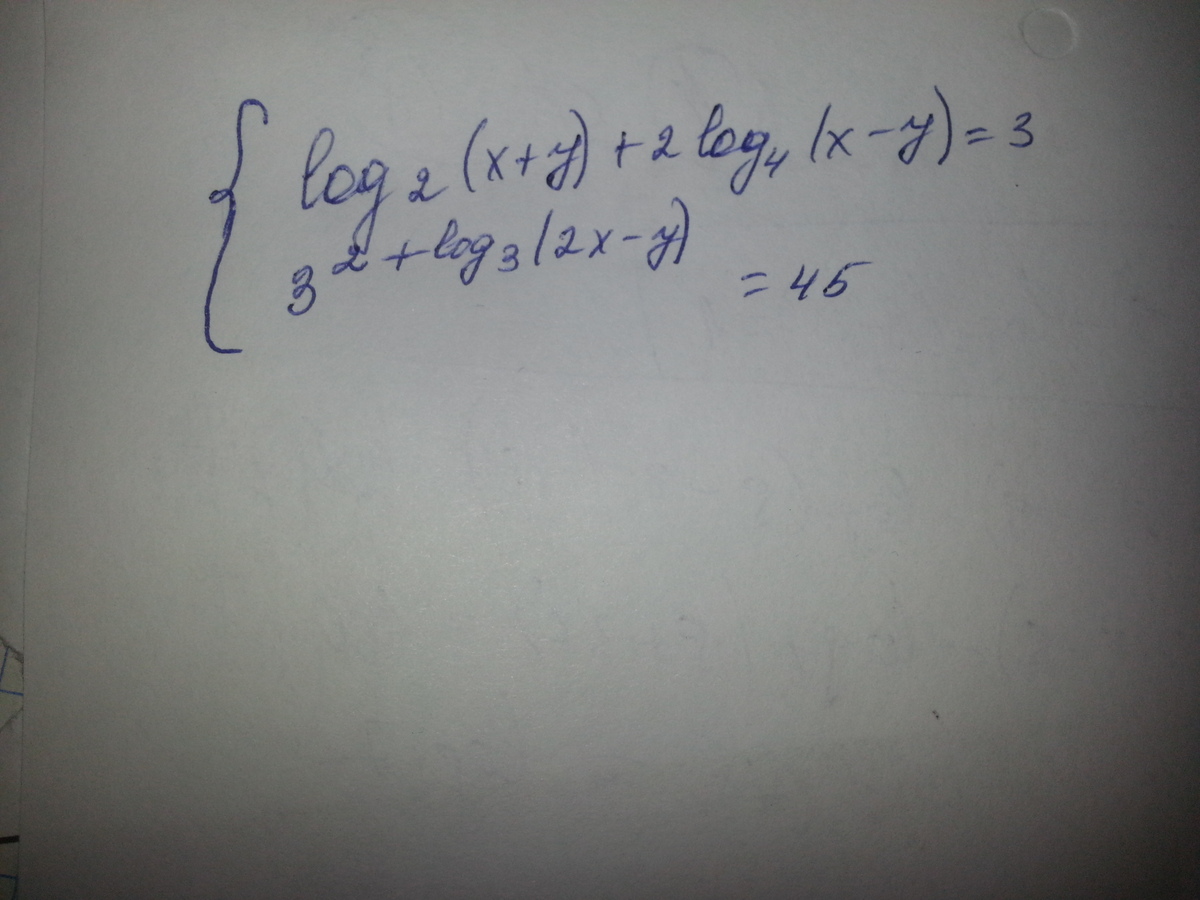
Ответы
Автор ответа:
0
имеем два ответа
Автор ответа:
0
зачем же так нервничать?
Автор ответа:
0
Так ничего не видно
Автор ответа:
0
обнови страницу, после правкм в техе необходимо обновить, у меня всё видно
Автор ответа:
0
амн
Автор ответа:
0
спасибо)
Автор ответа:
0
Если понравилось решение - нажимай "спасибо" и "лучший" (рядом с кнопкой "спасибо") :)
Приложения:
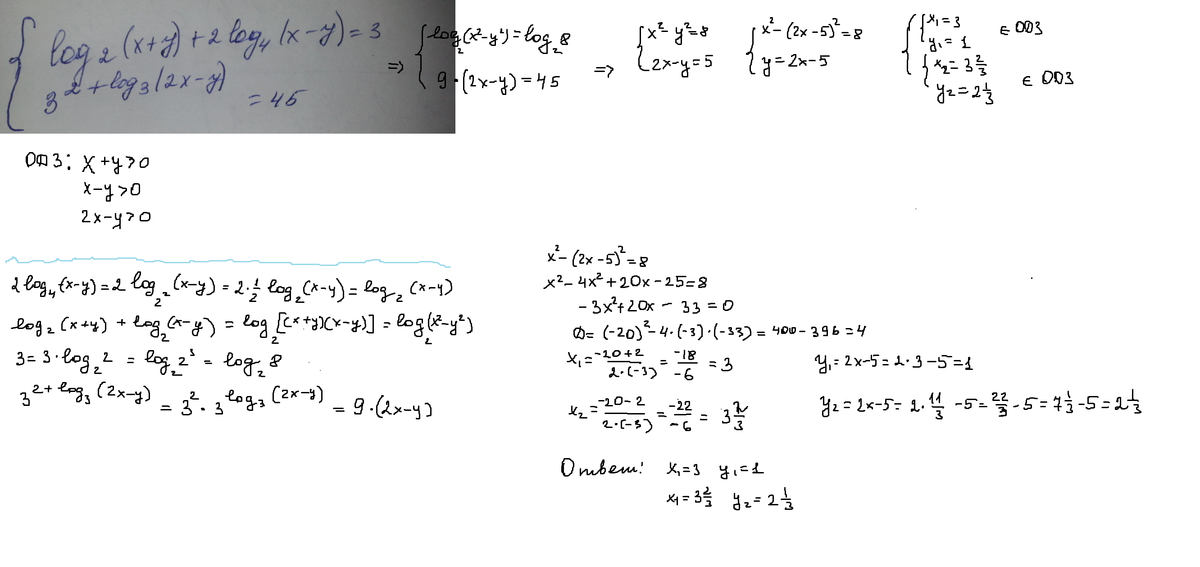
Автор ответа:
0
так это другое задание
Автор ответа:
0
???
Автор ответа:
0
обновите страницу (я просто несколько заданий решаю), не тот файл прикрепила.
Автор ответа:
0
спасибо)
Похожие вопросы
Предмет: Английский язык,
автор: god864054
Предмет: Английский язык,
автор: Аноним
Предмет: Обществознание,
автор: alenkins81
Предмет: Физика,
автор: paula2013
Предмет: Литература,
автор: stoyanoffa