Question

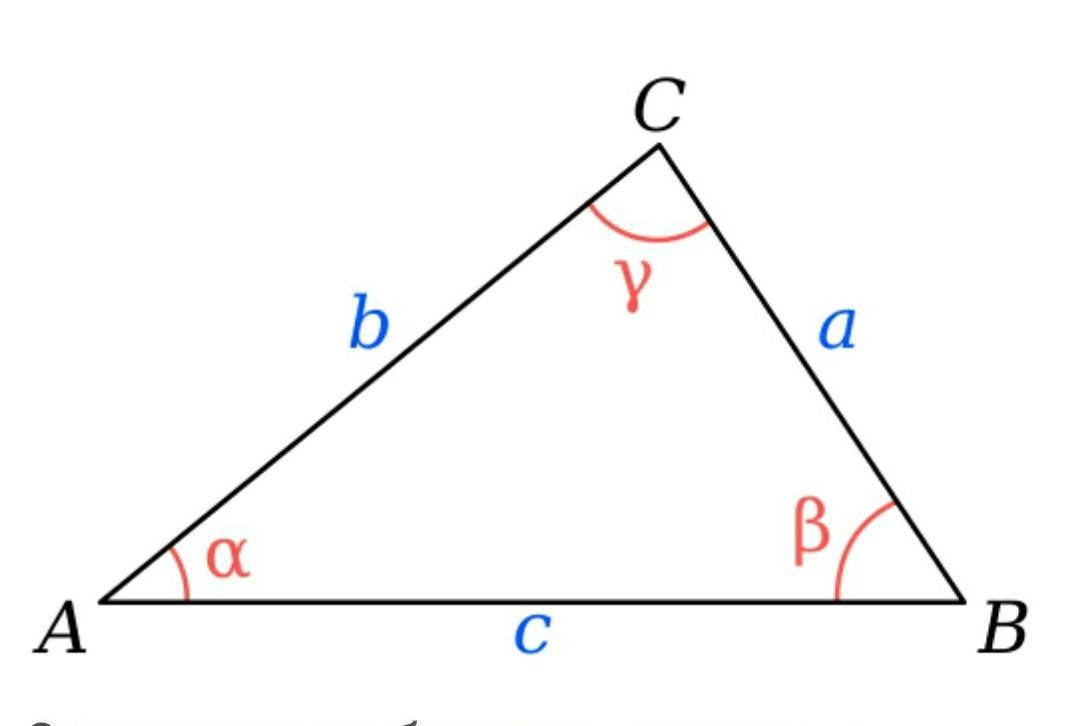
Знайти невідомі сторони і кути трикутника АВС,якщо ВС=6см,кут В=30°,кут С=45°

Answer 1

Ответ:

∠A=105°, AB≈4,4 см, АС≈3,1 см.

Объяснение:

Знайти невідомі сторони і кути трикутника АВС,якщо ВС=6см,кут В=30°,кут С=45°.

Значення тригонометричних функцій будемо знаходити за допомогою калькулятора й округлювати ці значення до сотих. Величини кутів будемо знаходити за допомогою калькулятора й округлювати ці значення до одиниць. Обчислюючи довжини сторін, результат будемо округлювати до десятих.

Дано: △АВС, ВС=6 см, ∠В=30°, ∠С=45°

Найти: ∠А, АВ, АС.

Решение

Позначимо а, b, c - довжини сторін трикутника, α, ß, γ - величини кутів, протилежних відповідно сторонам з довжинами a, b, c. Отже, а =6 см, ß = 30°, γ = 45°.

1.

Використовуючи теорему про суму кутів трикутника, отримаємо:

α = 180°- (ß + γ) = 180° - (30° + 45°) = 105°

Отже, ∠А=105°.

2.

За теоремою синусів:

$\dfrac{b}{\sin \beta } = \dfrac{a}{ \sin \alpha }$

$b = \dfrac{a \times \sin \beta }{ \sin \alpha } = \dfrac{6 \times \sin 30^\circ }{ \sin105^\circ } \approx \dfrac{6 \times 0,5}{0,97} \approx \bf3,1$

Отже, АС ≈ 3,1 см

3.

За теоремою синусів:

$\dfrac{c}{\sin \gamma } = \dfrac{a}{ \sin \alpha }$

$c = \dfrac{a \times \sin \gamma }{ \sin \alpha } =\dfrac{a \times \sin45^\circ }{ \sin105^\circ } \approx \dfrac{6 \times 0,71}{0,97} \approx \bf 4, 4$

Отже, АВ ≈ 4,4 см

#SPJ1