Задача 1.
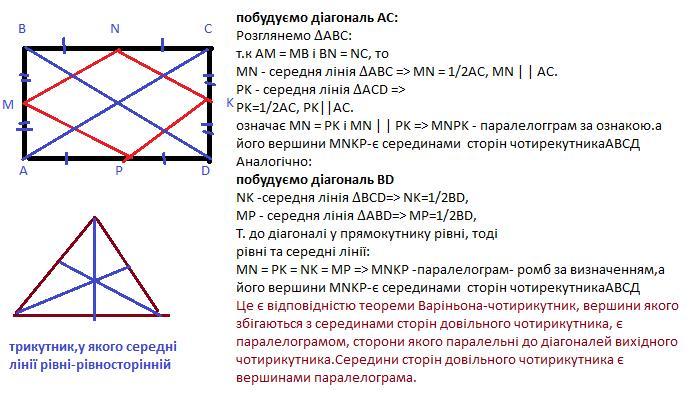
Визначте вид трикутника, у якому середні лінії рівні між собою.
Задача 2.
Доведіть, що середини сторін чотирикутника є вершинами паралелограма.
Ответы
Відповідь:
Задача 1.
Визначте вид трикутника, у якому середні лінії рівні між собою.
-це рівносторінній трикутник,
Якщо середні лінії трикутника рівні між собою, то трикутник рівносторонній. Якщо відрізок перетинає дві сторони трикутника і паралельний до третьої сторони, цей відрізок – середня лінія трикутника.
Задача 2.
Доведіть, що середини сторін чотирикутника є вершинами паралелограма.
У чотирекутнику АВСД побудуємо діагональ АС:
Розглянемо ∆АВС:
т.к АМ = МВ і ВN = NC, то
МN - середня лінія ∆АВС => МN = 1/2AC, MN | | AC.
PK - середня лінія ∆АСD =>
PK=1/2AC, PK||AC.
означає МN = PK і МN | | PK => MNPK - паралелогграм за ознакою.а його вершини MNKP-є серединами сторін чотирекутникаАВСД
Аналогічно:
побудуємо діагональ ВD
NK -середня лінія ∆ВСD=> NK=1/2BD,
MP - середня лінія ∆АВD=> MP=1/2BD,
T. до діагоналі у прямокутнику рівні, тоді
рівні та середні лінії:
MN = PK = NK = MP => MNKP -паралелограм- ромб за визначенням,а його вершини MNKP-є серединами сторін чотирекутникаАВСД
Це є відповідністю теореми Варіньона-чотирикутник, вершини якого збігаються з серединами сторін довільного чотирикутника, є паралелограмом, сторони якого паралельні до діагоналей вихідного чотирикутника.Середини сторін довільного чотирикутника є вершинами паралелограма.
Пояснення: