Предмет: Математика, автор: Моряка278

помогите пожалуйста :3

Приложения:

Ответы

Автор ответа: ewgenijbark

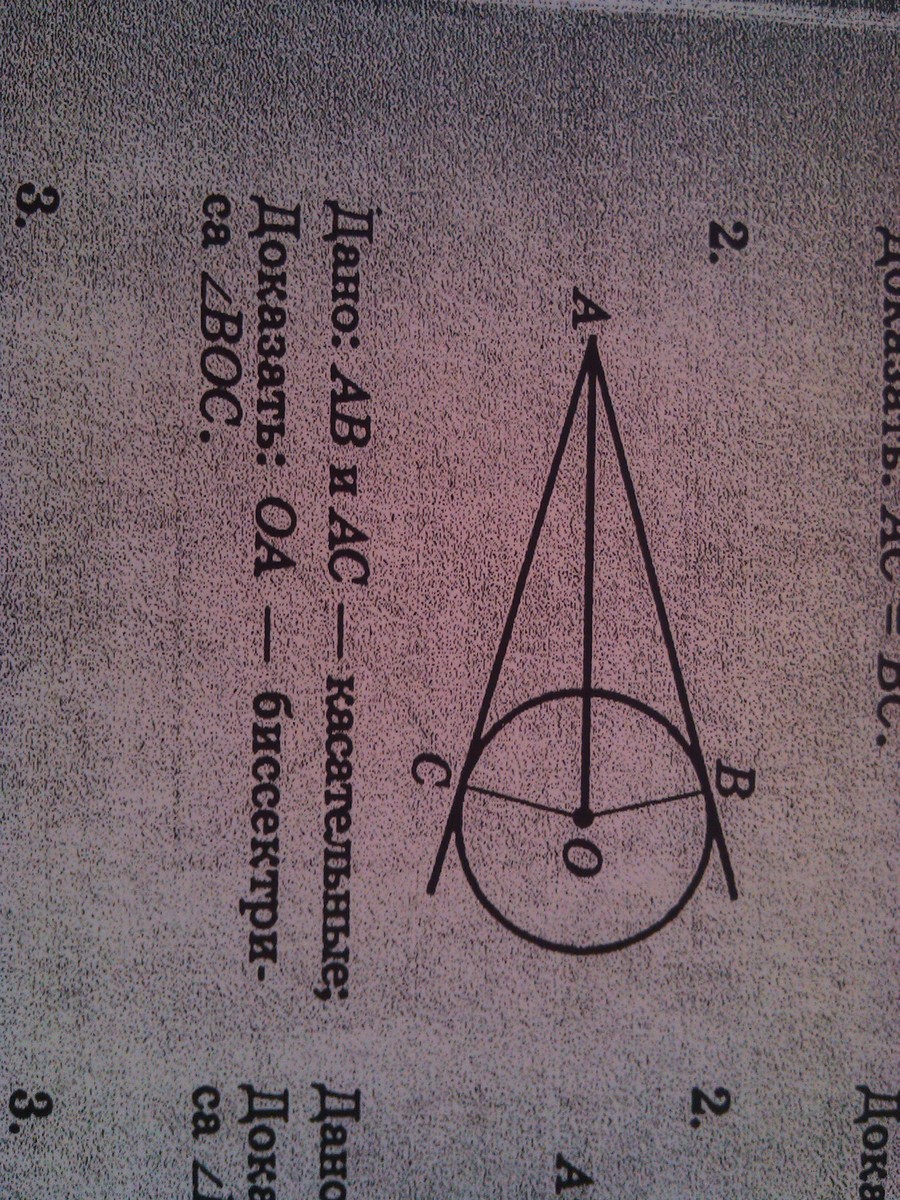
Теорема. Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными.

получается, что ОА-общая, АС=BC, OC=OB, значит треугольник AOC=AOB⇒<AOB=<AOC⇒OA биссектриса <BOC

Автор ответа: Моряка278

Спасибо

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Математика, автор: aleksyana3923

Выполнить сложение отрицательных чисел (с полным пояснением)

1. – 275 + (–362 ) =
2. –171+(–73 ) =
3. –367 + (–452) =
4. –254 + (–31 ) =
5. –445 + (–544) =
6. –227+(–91) =
7. –124 + (–32 ) =
8. –158 + (–12 ) =
9. –345 + (–42 )=
10. –543 +(–635 ) =
11. –225 + (–53 ) =
12. –435 + (–583 ) =
13. –131 + (–74 ) =
14. –154 + (–35 ) =
15. –234 + (–23 ) =

6 лет назад

Предмет: Русский язык, автор: annarudaqwerty

8. Обособленными членами предложения называются:
1) члены предложения, относящиеся к одному и тому же члену предложения, отвечающие на один вопрос, выполняющие одинаковую синтаксическую функцию;
2) члены предложения, выделяемые по смыслу и интонационно;
3) все члены предложения, кроме подлежащего и сказуемого

6 лет назад

Предмет: Математика, автор: abanovagulajym

34020:2
304020:2
3040 020:2
510015:5
5115.5
511500:500
936 003.7
9003.3
90030:30

6 лет назад

Предмет: Геометрия, автор: zzeenneekk

Основанием пирамиды служит равнобедренный треугольник, у которого равные стороны содержат по 39 см, а третья сторона 30 см. Двугранные углы при основании равны между собой, и каждый содержит 45°. Определить объём этой пирамиды.

9 лет назад

Предмет: Химия, автор: Софи123

помогите решить! пропанон ---> пропанол -2 напишите формулами

9 лет назад