Question

ОЧЕНЬ СРОЧНО!!! Помогите решить задачу(С ПОДРОБНЫМ РЕШЕНИЕМ!!)
Желательно с рисунком
Сторона AB ромба ABCD равна а, один из углов ромба равен 60 градусов. Через сторону АВ проведена плоскость альфа на расстоянии а/2 от точки D.

а) найдите расстояние от точки С до плоскости альфа

б) покажите на рисунке линейный угол двугранного угла DABM,M принадлежит альфа

в) найдите синус угла между плоскостью ромба и плоскостью альфа

Answer 1

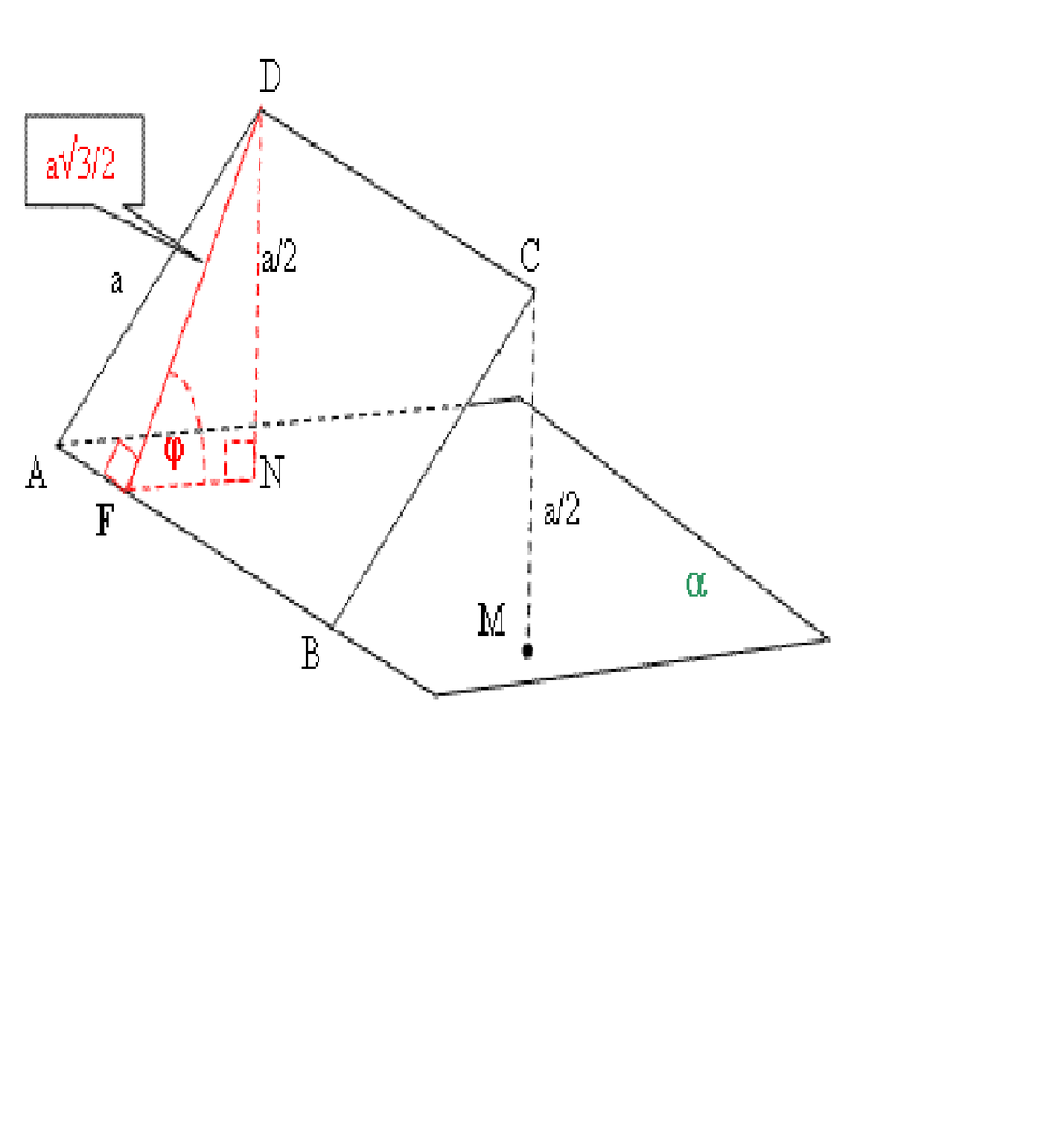
DN и CN - перпендикуляры, опущенные из из точек D и C на плоскость α.
 Длины этих перпендикуляров - расстояния от точек D и C до плоскости α.
а) расстояние от точки С до плоскости альфа = $frac{a}{2}$
б) линейный угол двугранного угла DABM, M принадлежит альфа -  угол φ
в) синус угла между плоскостью ромба и плоскостью альфа
 В ромбе проведем высоту DF, FN−проекция высоты FN на плоскость α, 
FN⊥AB (теорема о трех перпендикулярах).
 Угол DFN − линейный угол двугранного угла DABM, sinφ = $frac{1}{ sqrt{3} }$

Answer 2

а можно рисунок,если не сложно?

Answer 3

благодарю

Answer 4

И Вам всего хорошего