Dane: M₁ = 70x2 m. M₁₂ = 0,5x2 2 = 0,5M F-? F=G M₁ M2 8²
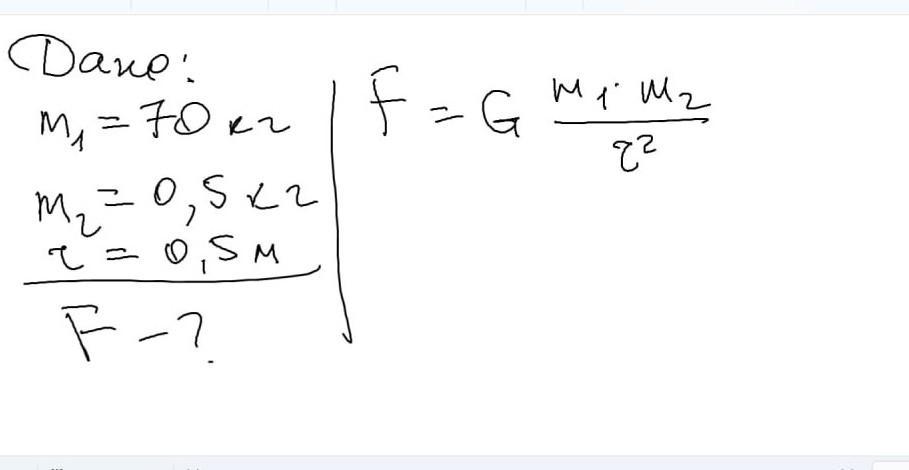
Ответы
Ответ:
Объяснение:
Судячи з наданих даних, вам потрібно обчислити силу гравітації (F), яка діє між двома масами M₁ і M₂ на відстані 8^2. Для цього ви можете використовувати закон всесвітнього тяжіння Ньютона, який має вигляд:
\[F = \frac{G \cdot M_1 \cdot M_2}{r^2},\]
де:
- F - сила гравітації,
- G - гравітаційна константа (приблизно \(6.674 \times 10^{-11} \, \text{м}^3/\text{kg} \cdot \text{s}^2\)),
- \(M_1\) - маса першого об'єкта (70x^2 м),
- \(M_2\) - маса другого об'єкта (0.5x^2 2 = 1x^2 м),
- \(r^2\) - квадрат відстані між цими об'єктами (8^2 = 64).
Підставляючи значення, отримаємо:
\[F = \frac{6.674 \times 10^{-11} \, \text{м}^3/\text{kg} \cdot \text{s}^2 \cdot (70x^2 \, \text{м}) \cdot (1x^2 \, \text{м})}{64 \, \text{м}^2}.\]
Зараз можемо обчислити це значення:
\[F = \frac{6.674 \times 10^{-11} \cdot 70 \cdot 1 \cdot x^4}{64} = \frac{6.674 \times 10^{-11} \cdot 70 \cdot x^4}{64}.\]
Отже, сила гравітації F дорівнює:
\[F = \frac{6.674 \times 10^{-11} \cdot 70 \cdot x^4}{64} \, \text{Н}.\]
Це значення сили гравітації між двома об'єктами при вказаних умовах.