Предмет: Геометрия,
автор: danilkramar5
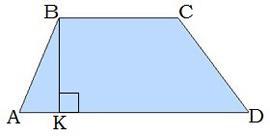
Бічна сторона AB трапеції ABCD утворює з більшою основою кут величиною 30°.
Обчисли висоту BK, якщо сторона AB дорівнює 92 см.
Висота BK дорівнює
Приложения:
Ответы
Автор ответа:
0
Объяснение:
∆АВК - прямоугольный:
∠А=30° ; АВ=92 см ;
Катет лежащий против угла 30° равен половине гипотенузы:
ВК=АВ:2=92:2=46 см
ответ: 46 см
Автор ответа:
1
Відповідь:
ВК = 46 см
Пояснення:
Дано:
АВСD - трапеція;
∠ВАD = 30*;
BK⊥AD; AB = 92 см;
Знайти:
ВК - ?
Розв‘язання:
BK⊥AD - за умовою, отже трикутник АВК - прямокутний (∠АКВ=90*), де АК і ВК - катети, АВ - гіпотенуза. ,
∠BAK = 30* (за умовою).
Катет, що лежить напроти кута 30*, дорівнює половині гіпотенузи. Звідси,
ВК = 1/2 • АВ
ВК = 1/2 • 92 = 46 (см)
Похожие вопросы
Предмет: Английский язык,
автор: sdalbna4
Предмет: Физика,
автор: stasgrecko09
Предмет: Математика,
автор: anglegidutcak
Предмет: Другие предметы,
автор: alla5361
Предмет: Литература,
автор: mariannafranc359