Question

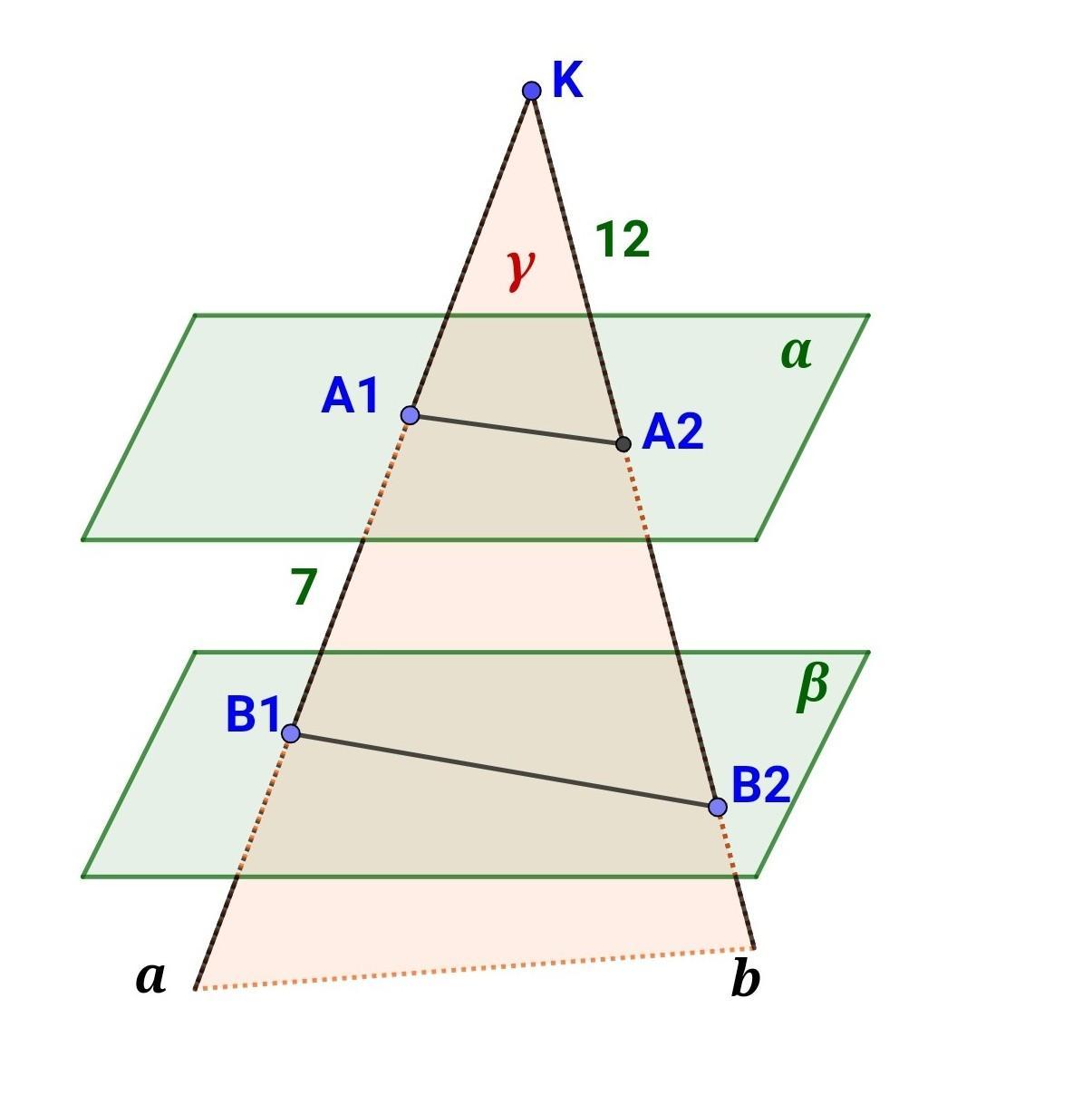
Через точку К проведены прямые а и в, пересекающие две параллельные плоскости α и β: первую в точках А1 и А2, вторую В1 и В2 соответственно. Известно что, В1В2:А1А2=4:3, А1В1=7см, КА2=12см. Вычислите КА1 и КВ2.​

Answer 1

Ответ:

КА1=21 см, КВ2= 16 см.

Объяснение:

Через точку К проведены прямые а и b, пересекающие две параллельные плоскости α и β: первую в точках А1 и А2, вторую В1 и В2 соответственно. Известно что, В1В2:А1А2=4:3, А1В1=7см, КА2=12см. Вычислите КА1 и КВ2.

1) a∩b = К, следовательно, через пересекающиеся прямые a и b проведем плоскость Ɣ. Эта плоскость пересекает плоскость α по прямой A1A2, а плоскость β по прямой В1В2.

2) По свойству параллельных плоскостей имеем А1А2 || В1В2.

3) Рассмотрим треугольники B1KB2 и A1KA2.

У них:

• ∠А1КА2=∠В1КВ2 – общий угол при вершине K;
• ∠КА1А2=∠КВ1В2 – как соответственные углы при параллельных прямых А1А2 и В1В2 и секущей а.

△B1KB2 ~ △A1KA2 (по двум углам).

4) Из подобия треугольников следует пропорциональность соответственных сторон:

$\bf\dfrac{B1K}{A1K} = \dfrac{B1B2}{A1A2} = \dfrac{KB2}{KA2}$

5) В1К=А1В1+А1К= 7+А1К, тогда:

$\dfrac{7 + A1K}{A1K} = \dfrac{4}{3}$

21+3•A1K=4•A1K

A1K=21 (см)

6)

$\dfrac{KB2}{12} = \dfrac{4}{3}$

$KB2 = \dfrac{4 \times 12}{3} = \bf 16$ (см)

#SPJ1