Question

Теория вероятность. На фото задача

Answer 1

Ответ:

а) $A=(A_1A_2+A_3+A_4A_5)A_6$

$\overline A=(\overline{A_1}+\overline{A_2})\overline{A_3}(\overline{A_4}+\overline{A_5})+\overline{A_6}$

б) 2,9%

Объяснение:

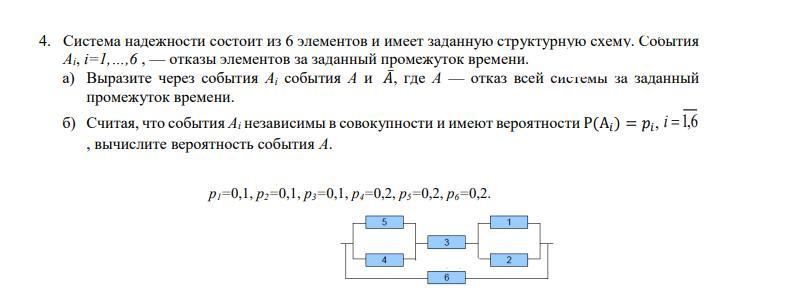
Необходимо найти, с какой вероятностью откажет система, заданная структурной схемой надежности.

а) Система откажет, если одновременно выйдет из строя устройство 6 и верхняя подсистема, состоящая из устройств 1–5.

Рассмотрим отдельно верхнюю подсистему. Для того, чтобы она отказала, требуется, чтобы:

не работали оба устройства 1–2

ИЛИ

не работало устройство 3

ИЛИ

не работали оба устройства 4–5

Будем обозначать $UV$ — одновременное выполнение U и V (логическое И), $U+V$ — условие того, что выполнено хотя бы одно из U или V (логическое ИЛИ), $\overline{U}$ — событие "U не выполнено". Для упрощений можно использовать тождества $\overline{\overline U}\equiv U$, $\overline{UV}=\overline U+\overline V$, $\overline{U+V}=\overline U\,\overline V$.

Сбой верхней подсистемы:

$A_1A_2+A_3+A_4A_5$

Отказ системы:

$(A_1A_2+A_3+A_4A_5)A_6$

Система работает:

$\overline{(A_1A_2+A_3+A_4A_5)A_6}=\overline{A_1A_2+A_3+A_4A_5}+\overline{A_6}=\\=\overline{A_1A_2}\,\overline{A_3}\,\overline{A_4A_5}+\overline{A_6}=(\overline{A_1}+\overline{A_2})\overline{A_3}(\overline{A_4}+\overline{A_5})+\overline{A_6}$

б) Чтобы найти вероятность отказа при условии, что все компоненты выходят из строя независимо, достаточно все $UV$ поменять на $p_U p_V$, $\overline{U}$ на $1-p_U$ и $U+V+W+\dots$ по формуле включений-исключений на $p_U+p_V+p_W+\dots-p_U p_V-p_U p_W-p_V p_W-\dots+p_U p_V p_W+\dots$

Вероятность того, что верхняя подсистема работает, соответствует выражению $\overline{A_1A_2}\,\overline{A_3}\,\overline{A_4A_5}$:

(1 − p₁ p₂) (1 − p₃) (1 − p₄ p₅) = 0,85536

Вероятность отказа верхней подсистемы:

1 - 0,85536 = 0,14464

Вероятность отказа всей системы:

0,14464 · 0,2 = 0,028928 ≅ 2,9%

Если вы из секты нелюбителей процентов, можно оставить ответ в виде десятичной дроби.