3. Найдите множество точек координатной плоскости, заданных системой неравенств:
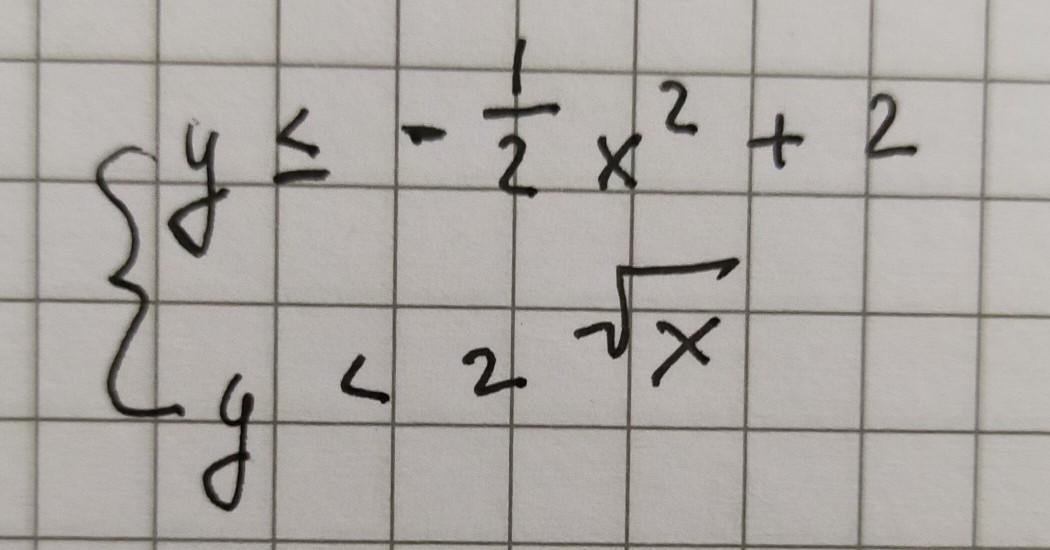
Ответы
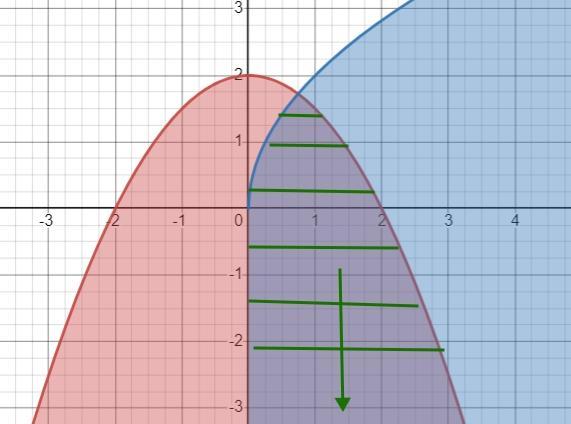
Ответ:
На рисунке
Объяснение:
Строим параболу
y = a(x-k)² + b
Коэффициент a при х² отрицательный - ветви параболы вниз.
Вершина параболы, поскольку k=0 х и b = 2, - точка (0; 2)
Нули параболы (-2; 0) и (2; 0) (парабола расширяется относительно графика y=x² по оси ОХ в 2 раза)
Смотрим, где область удовлетворяющая неравенству.
Эта область внутри параболы.
Теперь строим параболу
Ветви параболы вправо.
Только часть, расположенная в первой четверти.
Парабола расширяется по оси OY в 2 раза по сравнению с у = √х.
Можно взять несколько точек, если нужна точность.
Где область, удовлетворяющая исходному неравенству?
Она расположена внизу параболы и ограничена слева прямой х=0.
Таким образом, на пересечении наших областей мы получим геометрическое место точек, удовлетворяющее заданной системе.