Предмет: Математика,
автор: eyler15
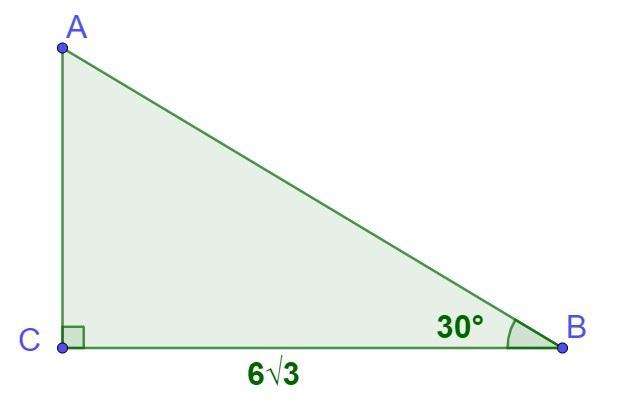
Найдите площадь прямоугольного треугольника ABC, если угол ABC равен 30°, CB катет 6 корень 3
Ответы
Автор ответа:
1
Ответ:
Площадь ΔАВС равна 18√3 кв. ед.
Пошаговое объяснение:
Найдите площадь прямоугольного треугольника ABC, если угол ABC равен 30°, а катет CB 6√3.
Дано: ΔАВС, ∠С=90°, ∠АВС=30°, СВ=6√3
Найти: S(ΔАВС)
Решение
1. По определению тангенса острого угла прямоугольного треугольника найдём катет АС.
AC = CB · tg ∠ABC = 6√3 · tg 30° =
(ед)
2. Найдём площадь ΔАВС как половину произведения его катетов:
(кв. ед)
Ответ: 18√3 кв.ед.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Русский язык,
автор: Iramzuuuk
Предмет: Русский язык,
автор: erasylabbas00
Предмет: Химия,
автор: mojk8964
Предмет: Другие предметы,
автор: khozhabaev74ak