Предмет: Геометрия,
автор: Bogdanychteren
В прямоугольном треугольнике ABC AC = a, угол B = 30° . Через вершину прямого угла проведена окружность, касающаяся AB, и отсекающая от катетов равные хорды. Найти ее радиус.
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
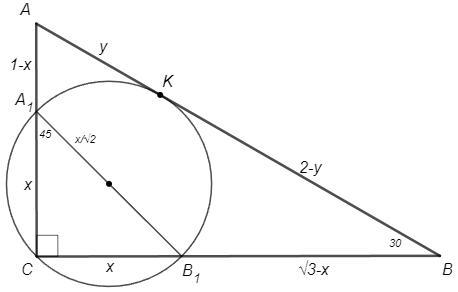
Пусть a=1, тогда AC=1, BC=√3, AB=2
CA1=CB1=x, AK=y
По т о касательной и секущей
AK^2 =AC*AA1 => y^2 =1-x
BK^2 =BC*BB1 => (2-y)^2 =√3(√3-x)
4 -4√(1-x) +(1-x) =3 -√3x
4√(1-x) = x(√3-1) +2
16(1-x) = x^2(4-2√3) +4x(√3-1) +4
8(1-x) = x^2(2-√3) +2x(√3-1) +2
x^2(2-√3) +2x(√3+3) -6 =0
x = -(√3+3) +√( (√3+3)^2 +(2-√3)6 ) /(2-√3) //положительный корень
√(3 +6√3 +9 +12 -6√3) -√3 -3 /(2-√3)
(2√6-√3-3)/(2-√3) = (2√6-√3-3)(2+√3) = 4√6 -5√3 +6√2 -9
A1B1C -р/б прямоугольный, с углами 45-90
т синусов: 2R =x/sin45 => R =x/√2 = 4√3 -5√3/√2 +6 -9/√2
Ответ умножим на a
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ariktrush12
Предмет: Қазақ тiлi,
автор: ayazhanegenbay43
Предмет: Математика,
автор: gogorianani
Предмет: Обществознание,
автор: kani021
Предмет: Химия,
автор: YurevSay