У кулю радіусом 3 вписано конус найбільшого об'єму. Визначити висоту цього конуса.
Ответы
Ответ:
Пошаговое объяснение:
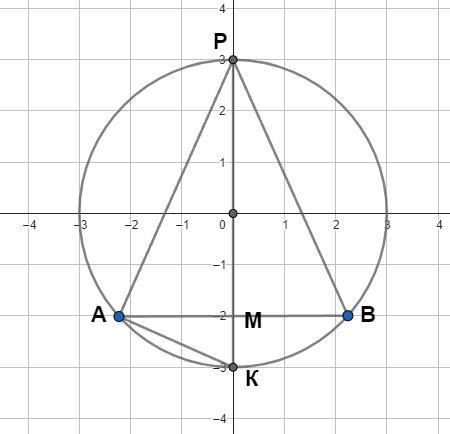
Возьмем сечение сферы плоскостью, проходящей через её центр O. В сечении мы получим окружность и вписанный в нее равнобедренный треугольник.
ΔАРВ. он прямоугольный. ∠РАВ = 90°. Из этого угла опустим высоту АМ на гипотенузу РК.
Теперь по свойству высоты из прямого угла мы можем записать
(ВМ)² = РМ*МК.
Посмотрим, что у нас получится в терминах окружности
r - радиус основания конуса.
РМ = h - высота конуса.
РК = 2R - диаметр круга (R - радиус круга)
запишем наше свойство так:
r² = h(2R-h)
Объем конуса запишем как функцию от h
где h изменяется в переделах (0; 2R)
Нам требуется найти, при каком значении h функция V(h) принимает максимальное значение.
Внесем h² под скобки и возьмем производную.
приравняем ее к нулю и найдем критические точки
h₁ =0 не входит в наш промежуток. поэтому наше решение h₂
Подставим туда значение R=3 для нашей задачи и получим
Таким образом максимальный объем конуса будет достигнут при высоте конуса равной 4