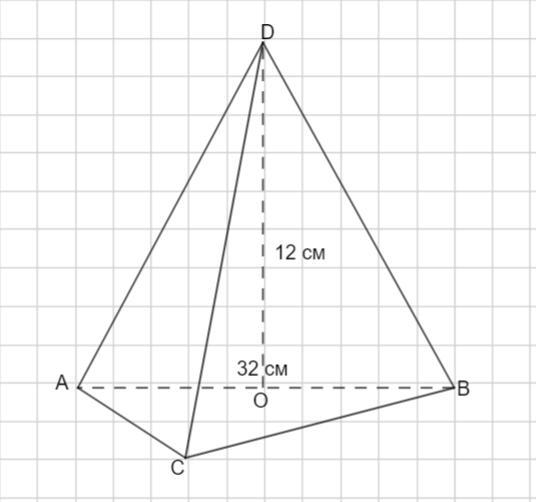
Основою піраміди є прямокутний трикутник, гіпотенуза якого дорівнює 32 см. Висота піраміди дорівнює 12 см. Знайдіть бічні ребра піраміди, якщо вони утворюють рівні кути з площиною основи.
Ответы
Ответ:
20 см
Объяснение:
Основанием пирамиды является прямоугольный треугольник, гипотенуза которого равна 32 см. Высота пирамиды равна 12 см. Найти боковые ребра пирамиды, если они образуют равные углы с плоскостью основания.
Пусть дана пирамида DABC. ΔАВС - прямоугольный. Так как по условию все боковые ребра образуют с плоскостью основания равные углы , то вершина D проектируется в центр описанной около ΔАВС окружности. Если ΔАВС - прямоугольный, то центр описанной окружности - это середина гипотенузы. Тогда DО - высота, DО = 12 см. Точка О - середина гипотенузы АВ. АО = ВО = 32 : 2 = 16 см.
Рассмотрим ΔАОD - прямоугольный и применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
АD²= АО²+ ОD²;
АD² = 16² +12² = 256 +144 = 400;
АD =√400= 20 см.
Значит, каждое боковое ребро пирамиды равно 20 см.
#SPJ1