Предмет: Математика,
автор: study2023
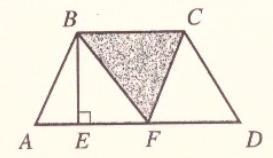
Площадь трапеции SABCD = 30 м^2, BE = 6 м и AD = 7 м. Вычисляй площадь треугольника BCF!
Приложения:
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
По определению трапеции, её площадь равняется полусумме оснований, умноженной на высоту
Найдём отсюда BC
По определению треугольника, его площадь равняется произведению основания на высоту, поделённое пополам
Найдём отсюда площадь треугольника BCF
Похожие вопросы
Предмет: Русский язык,
автор: gavharbotir
Предмет: Литература,
автор: arikl5314
Предмет: Русский язык,
автор: damik0728
Предмет: Математика,
автор: arzamasskiiin3742