Предмет: Алгебра,
автор: viktoriakarpenko6969
допоможіть спростити вираз:
Приложения:
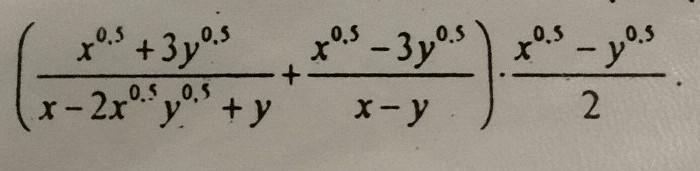
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: lizadiana234
Предмет: Биология,
автор: taisiadance
Предмет: Математика,
автор: vitalijgladilin1
Предмет: Математика,
автор: vovapachin78