Question

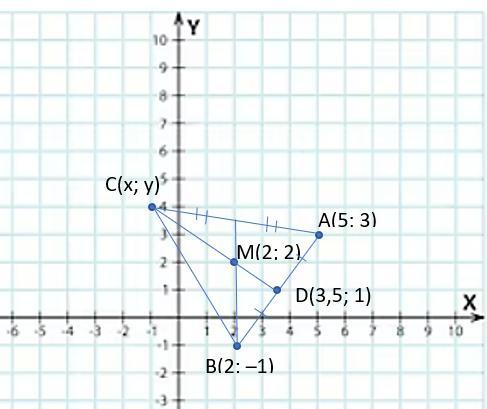
Если медианы треугольника ABC с вершинами A(5,3) и B(2,-1) пересекаются в точке M(2,2), найти координаты его вершины C(x,y)

Answer 1

Ответ:

Координаты третьей вершины: C(-1; 4)

Объяснение:

Информация. 1) Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

2) Координаты (x₀; y₀) середины отрезка с вершинами в точках A(x₁;y₁) и B(x₂;y₂) определяется по формулам:

$\tt x_0=\dfrac{x_1+x_2}{2}; \;\;\; y_0=\dfrac{y_1+y_2}{2}$.

3) Все три медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины.

4) Если известны две точки плоскости A(x₁;y₁) и B(x₂;y₂) , то координаты точки O(x₃; y₃), которая делит отрезок AB в отношении k=AO:OB, выражаются формулами:

$\tt x_3=\dfrac{x_1+k \cdot x_2}{1+k}; \;\;\; y_3=\dfrac{y_1+k \cdot y_2}{1+k}.$

Решение. Так как медиана AD делит сторону AB пополам (см. рисунок), то определим по формулам 2) координаты точки D(x₀; y₀):

$\tt x_0=\dfrac{5+2}{2}=3,5; \;\;\; y_0=\dfrac{3+(-1)}{2}=1.$

Отсюда D(3,5; 1).

По свойству 3) точкой пересечения медиан M(x₃; y₃)=M(2; 2) медиана AD делится в отношении k = 2:1 = 2. Поэтому применив формулы 4) определим координаты точки C(x; y):

$\tt 2=\dfrac{x+2 \cdot 3,5}{1+2}; \;\;\; 2=\dfrac{y+2 \cdot 1}{1+3} \\\\x=2 \cdot 3-7=-1; \;\;\; y=2 \cdot 3-2=4.$

Значит, C(-1; 4).

#SPJ1