6) (2x - 5)² + 1 = 0; B) x⁶ - 1 = 0.
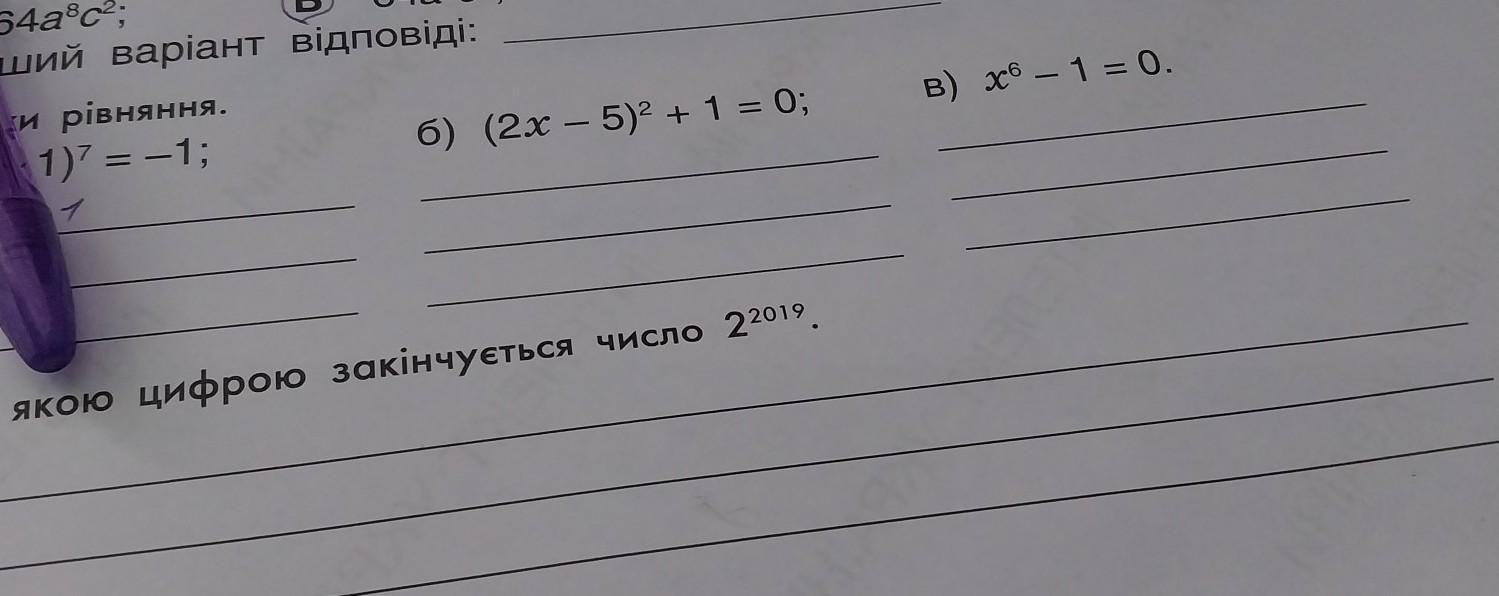
Ответы
Ответ:
A) Давайте розв'яжемо рівняння (2x - 5)² + 1 = 0.
(2x - 5)² + 1 = 0
Спочатку віднімемо 1 з обох сторін:
(2x - 5)² = -1
Тепер ми маємо квадратний доданок на лівій стороні рівняння. Оскільки квадратний доданок завжди не від'ємний, то він не може дорівнювати -1. Отже, це рівняння не має розв'язків у множині дійсних чисел.
B) Давайте розв'яжемо рівняння x⁶ - 1 = 0.
x⁶ - 1 = 0
Для розв'язання цього рівняння використовуємо різницю квадратів:
(x³)² - 1² = 0
Тепер ми маємо різницю квадратів:
(x³ - 1)(x³ + 1) = 0
Розглянемо обидва множники:
x³ - 1 = 0
Додамо 1 до обох сторін:
x³ = 1
Знаходимо кубічний корінь:
x = 1
x³ + 1 = 0
Віднімемо 1 від обох сторін:
x³ = -1
Знаходимо кубічний корінь:
x = -1
Таким чином, рівняння має два розв'язки: x = 1 і x = -1.
Объяснение:
Ответ:
Объяснение:
б)
(2х - 5)² + 1 = 0
(2х - 5)(2х - 5) + 1 = 0
4х² - 10х - 10х + 25 + 1 = 0
4х² - 20х + 26 = 0 | : 2
2х² - 10х + 13 = 0
D = 10² - 4 * 2 * 13 = 100 - 104 = - 4
D < 0 рішення немає
в)
х⁶ - 1 = 0
х⁶ = 1
х = ± 1