Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовності.
Приложения:
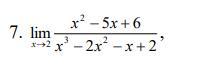
Ответы
Автор ответа:
1
Ответ:
При раскрытии неопределённости типа 0/0 раскладываем на множители многочлены .
Приложения:

fctdgsygfdhngfxzgsac:
спасибо большое)) у меня в профиле еще несколько заданий по границам есть, прошу помогите
Похожие вопросы
Предмет: Биология,
автор: kixxxq
Предмет: География,
автор: yunafox28
Предмет: Право,
автор: maksimka327984798
Предмет: Информатика,
автор: kornienkova2007
Предмет: Математика,
автор: maksimsahab07