Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовності.
Приложения:
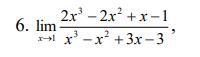
Ответы
Автор ответа:
1
Ответ:
Объяснение:
fctdgsygfdhngfxzgsac:
дуже дякую)
Похожие вопросы
Предмет: География,
автор: yunafox28
Предмет: Право,
автор: maksimka327984798
Предмет: Другие предметы,
автор: 4Lili34
Предмет: Математика,
автор: maksimsahab07
Предмет: Биология,
автор: nikitakaryanov