Question

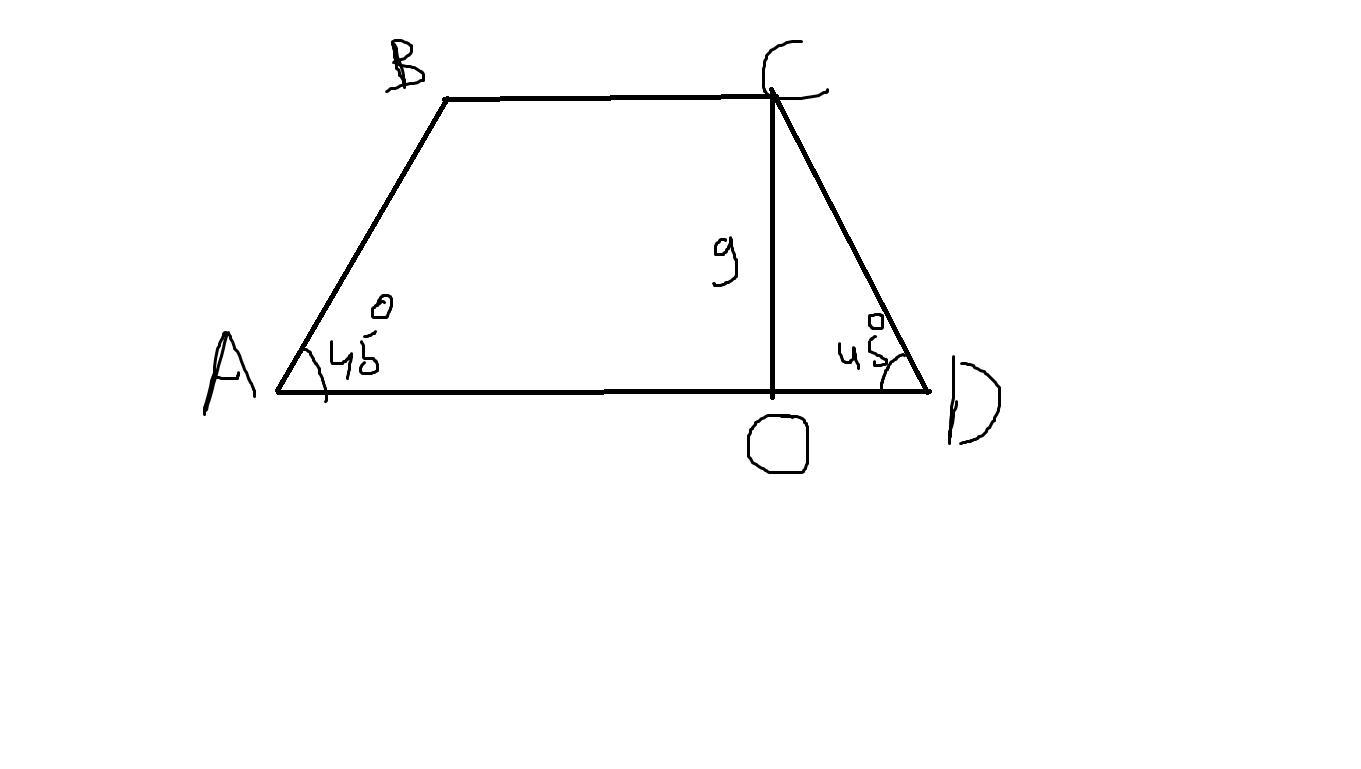
3. Острый угол равнобедренной трапеции равен 45°, высота 9 дм, а сумма оснований 30 дм, - Найдите длины оснований трапеции.​

Answer 1

Відповідь:

Пояснення:

1)Найдем OD:

tga=OC/OD

OD=OC/tga=9/tg45°=9дм

2)Пусть меньшее основание равно х, тогда большее - х+18 (х+9+9)

х+х+18=30

2х+18=30

2х=12

х=6 -меньшее основание ВС

х+18=6+18=24- большее основание AD

Answer 2

Ответ:

6, 24 дм

Объяснение:

Дано: ABCD - р/б трапеция

∠D=45°

AE - высота; AE= 9 дм

AB+DC= 30 дм

Найти: AB; DC

Решение:

AE - высота (из условия) => EC = AB+DC/2 (свойство р/б трапеции) = 30/2 = 15 (дм)

Рассмотрим ΔDAE

=> ∠DEA = 90°

∠DAE = 180° - (∠EDA - ∠DEA) = 180° - (45°+90°) = 45° (теорема о сумме углов треугольника)

Следовательно, ΔDEA - р/б (т.к. ∠EDA=∠DAE=45°) => DE=AE=9 (дм)

DC = DE+EC = 9 + 15= 24 (дм) => AB = 30 - 24 = 6 (дм)