Предмет: Алгебра,
автор: polinasidorcuk59
3. Доведіть тотожність
Приложения:
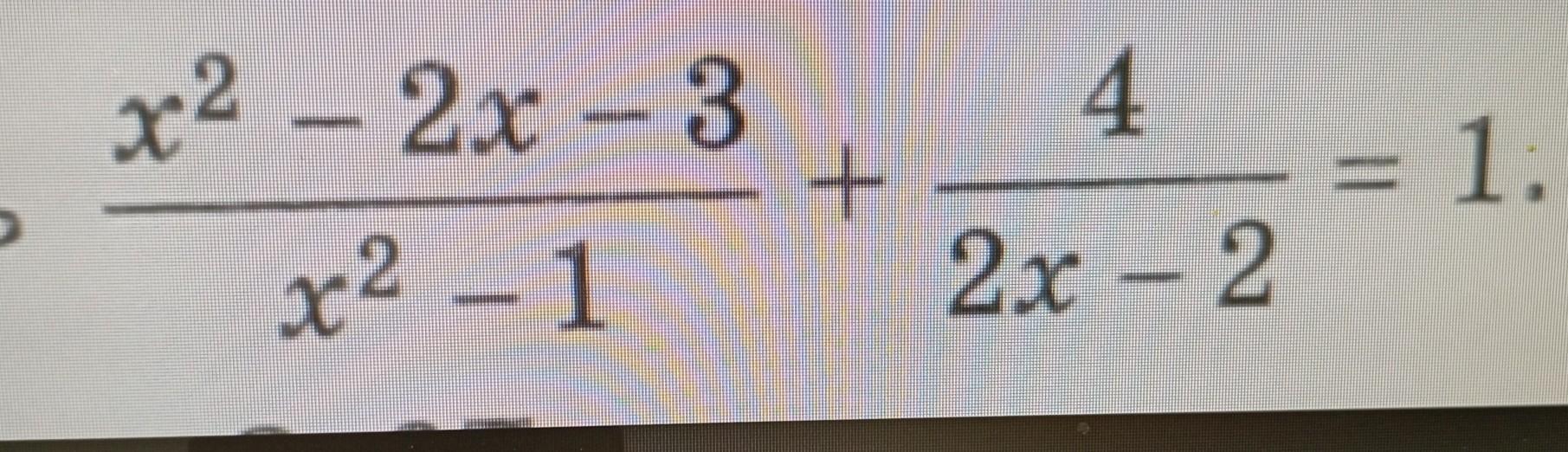
Ответы
Автор ответа:
0
Для доведення тотожності, спочатку приведемо обидві частини рівняння до спільного знаменника:
(x² - 2x - 3) / (x² - 1) + 4 / (2x - 2) = 1
Знаменник першого доданка можна розкласти на множники:
(x² - 2x - 3) = (x - 3)(x + 1)
Знаменник другого доданка можна спростити:
(2x - 2) = 2(x - 1)
Тепер перепишемо рівняння з врахуванням цих спрощень:
(x - 3)(x + 1) / (x² - 1) + 4 / (2(x - 1)) = 1
Тепер приведемо знаменники до спільного знаменника, який буде (x² - 1)(2(x - 1)):
[(x - 3)(x + 1)(2(x - 1)) + 4(x² - 1)] / [(x² - 1)(2(x - 1))] = 1
Помножимо чисельник першого доданка:
[(2x² - 2)(x - 3)(x + 1) + 4(x² - 1)] / [(x² - 1)(2(x - 1))] = 1
Розкриємо дужки в чисельнику:
[(2x² - 2)(x² - 2x - 3) + 4x² - 4] / [(x² - 1)(2x - 2)] = 1
Помножимо першу дужку на другу:
(2x⁴ - 4x³ - 6x² - 2x² + 4x + 6 + 4x² - 4) / [(x² - 1)(2x - 2)] = 1
Спростимо чисельник:
(2x⁴ - 4x³ - 4x² + 4x + 2) / [(x² - 1)(2x - 2)] = 1
Тепер спростимо знаменник:
(x² - 1)(2x - 2) = (x - 1)(x + 1)(2(x - 1)) = 2(x - 1)(x + 1)(x - 1) = 2(x - 1)²(x + 1)
Підставимо це у рівняння:
(2x⁴ - 4x³ - 4x² + 4x + 2) / [2(x - 1)²(x + 1)] = 1
Помножимо обидві частини рівняння на знаменник:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2(x - 1)²(x + 1)
Розкриємо дужки у правій частині:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2(x² - 2x + 1)(x + 1)
Спростимо праву частину:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2(x⁴ - 2x³ + x² + x² - 2x + 1)
Розкриємо дужки:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2x⁴ - 4x³ + 2x² + 2x² - 4x + 2
Спростимо рівняння:
0 = 0
Отримали тотожність, що означає, що початкове рівняння є тотожністю і справедливе для будь-якого значення x.
(x² - 2x - 3) / (x² - 1) + 4 / (2x - 2) = 1
Знаменник першого доданка можна розкласти на множники:
(x² - 2x - 3) = (x - 3)(x + 1)
Знаменник другого доданка можна спростити:
(2x - 2) = 2(x - 1)
Тепер перепишемо рівняння з врахуванням цих спрощень:
(x - 3)(x + 1) / (x² - 1) + 4 / (2(x - 1)) = 1
Тепер приведемо знаменники до спільного знаменника, який буде (x² - 1)(2(x - 1)):
[(x - 3)(x + 1)(2(x - 1)) + 4(x² - 1)] / [(x² - 1)(2(x - 1))] = 1
Помножимо чисельник першого доданка:
[(2x² - 2)(x - 3)(x + 1) + 4(x² - 1)] / [(x² - 1)(2(x - 1))] = 1
Розкриємо дужки в чисельнику:
[(2x² - 2)(x² - 2x - 3) + 4x² - 4] / [(x² - 1)(2x - 2)] = 1
Помножимо першу дужку на другу:
(2x⁴ - 4x³ - 6x² - 2x² + 4x + 6 + 4x² - 4) / [(x² - 1)(2x - 2)] = 1
Спростимо чисельник:
(2x⁴ - 4x³ - 4x² + 4x + 2) / [(x² - 1)(2x - 2)] = 1
Тепер спростимо знаменник:
(x² - 1)(2x - 2) = (x - 1)(x + 1)(2(x - 1)) = 2(x - 1)(x + 1)(x - 1) = 2(x - 1)²(x + 1)
Підставимо це у рівняння:
(2x⁴ - 4x³ - 4x² + 4x + 2) / [2(x - 1)²(x + 1)] = 1
Помножимо обидві частини рівняння на знаменник:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2(x - 1)²(x + 1)
Розкриємо дужки у правій частині:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2(x² - 2x + 1)(x + 1)
Спростимо праву частину:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2(x⁴ - 2x³ + x² + x² - 2x + 1)
Розкриємо дужки:
2x⁴ - 4x³ - 4x² + 4x + 2 = 2x⁴ - 4x³ + 2x² + 2x² - 4x + 2
Спростимо рівняння:
0 = 0
Отримали тотожність, що означає, що початкове рівняння є тотожністю і справедливе для будь-якого значення x.
Похожие вопросы
Предмет: Английский язык,
автор: hwanh
Предмет: Математика,
автор: coca111pup
Предмет: Биология,
автор: dendiluckk
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Sashaanimeme