Предмет: Алгебра, автор: elizabethmajorka

Будь ласка зробіть буду дуже вдячна

Приложения:

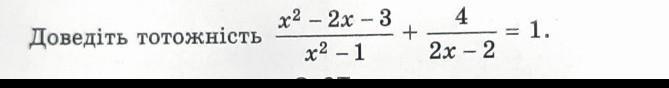
Ответы

Автор ответа: imaska9865

Ответ:

$\frac{ {x}^{2} - 2x - 3 }{ {x}^{2} - 1} + \frac{4}{2x - 2} = \frac{ {x}^{2} - 2x - 3}{(x - 1)(x + 1)} + \frac{4}{2(x - 1)} = \frac{ 2({x}^{2} - 2x - 3) }{2(x - 1)(x + 1)} + \frac{4(x + 1)}{2(x - 1)(x + 1)} = \frac{2 {x}^{2} - 4x - 6 + 4x + 4 }{2(x - 1)(x + 1)} = \frac{2 {x}^{2} - 2}{2(x - 1)(x + 1)} = \frac{2( {x}^{2} - 1)}{2(x - 1)(x + 1)} = \frac{2( {x}^{2} - 1) }{2( {x}^{2} - 1) } = 1$

elizabethmajorka: Это полный ответ ?? это все нужно писать?

imaska9865: можете добавить "торжество доказано" в конце, но это не является обязательным

elizabethmajorka: спасибо

imaska9865: это не обязательно потому что суть задания как раз дойти до ответа предложенного в задании, по этому писать не обязательно

imaska9865: всегда рада помочь

Автор ответа: Universalka

$\displaystyle\bf\\\frac{x^{2} -2x-3}{x^{2} -1} +\frac{4}{2x-2} = \frac{x^{2} -2x-3}{(x -1)\cdot(x+1)}+\frac{4}{2\cdot(x-1)} = \\\\\\=\frac{x^{2} -2x-3}{(x-1)\cdot(x+1)} +\frac{2}{x-1} = \frac{x^{2}-2x-3+2\cdot(x+1) }{x^{2} -1} =\\\\\\=\frac{x^{2}-2x-3+2x+2 }{x^{2} -1} =\frac{x^{2}-1 }{x^{2} -1} =1\\\\\\1=1$