Предмет: Геометрия,
автор: cvb115
Площа перерізу прямокутного паралелепіпеда площиною, що проходить через протилежні бічні ребра, дорівнює 24 см2, а сторони основи – 3 і 4 см. Знайдіть:
а) кут нахилу діагоналі паралелепіпеда до площини основи;
б) площу перерізу паралелепіпеда площиною, що проходить через бічне ребро під кутом 30° до більшої бічної грані.
Ответы
Автор ответа:
6
Ответ:
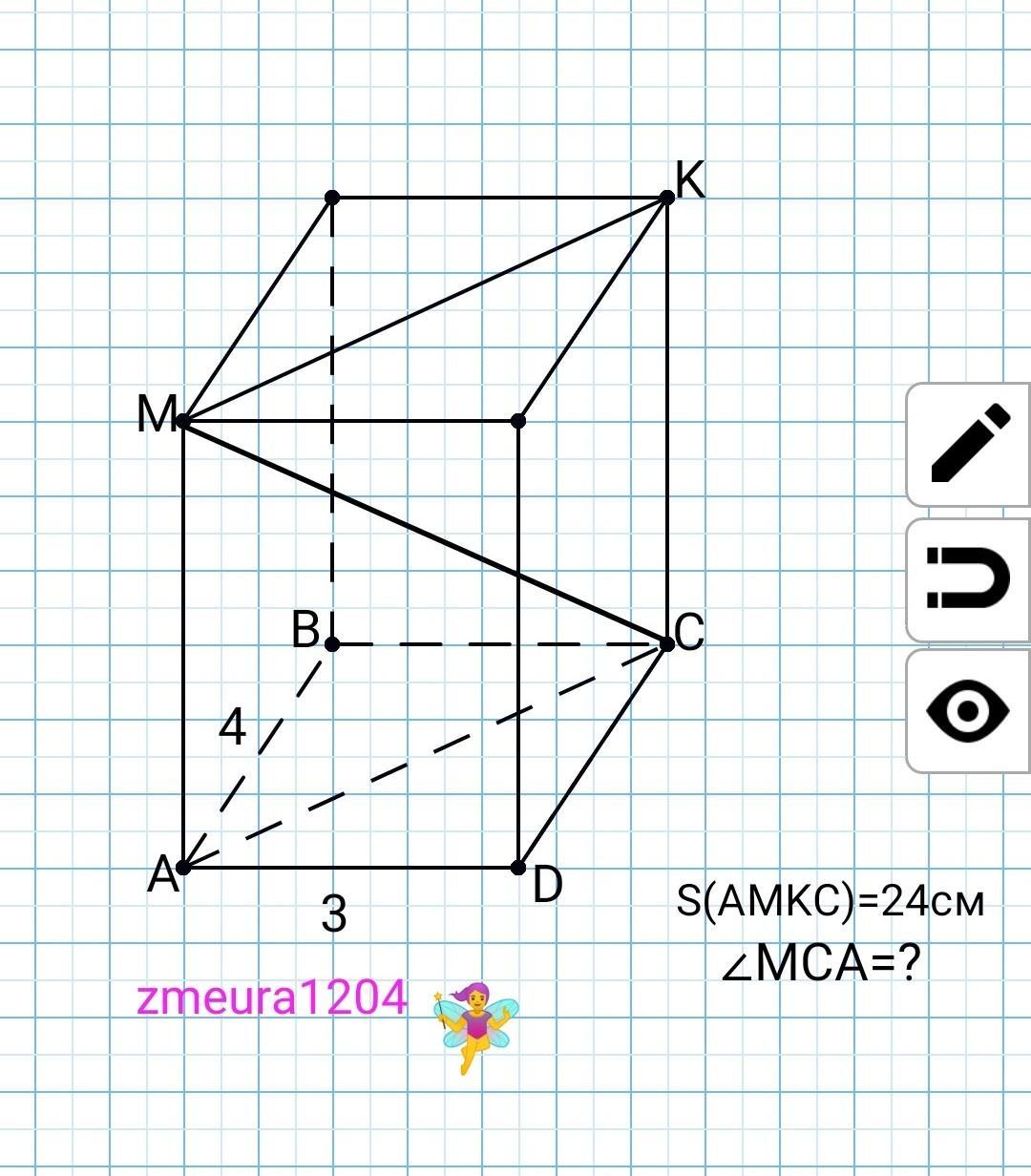
1) ∠МСА=arctg0,96
2) Площа перерізу дорівнює 8√3см²
Объяснение:
1)
∆ACD- прямокутний трикутник
Теорема Піфагора:
АС=√(АD²+DC²)=√(3²+4²)=
=5см.
S(AMKC)=AC*AM;
AM=S(AMKC)/AC=24/5=4,8 см.
tg∠МСА=MA/AC=4,8/5=0,96
∠MCA=arctg0,96 (табл. Брадіса на допомогу)
_____________
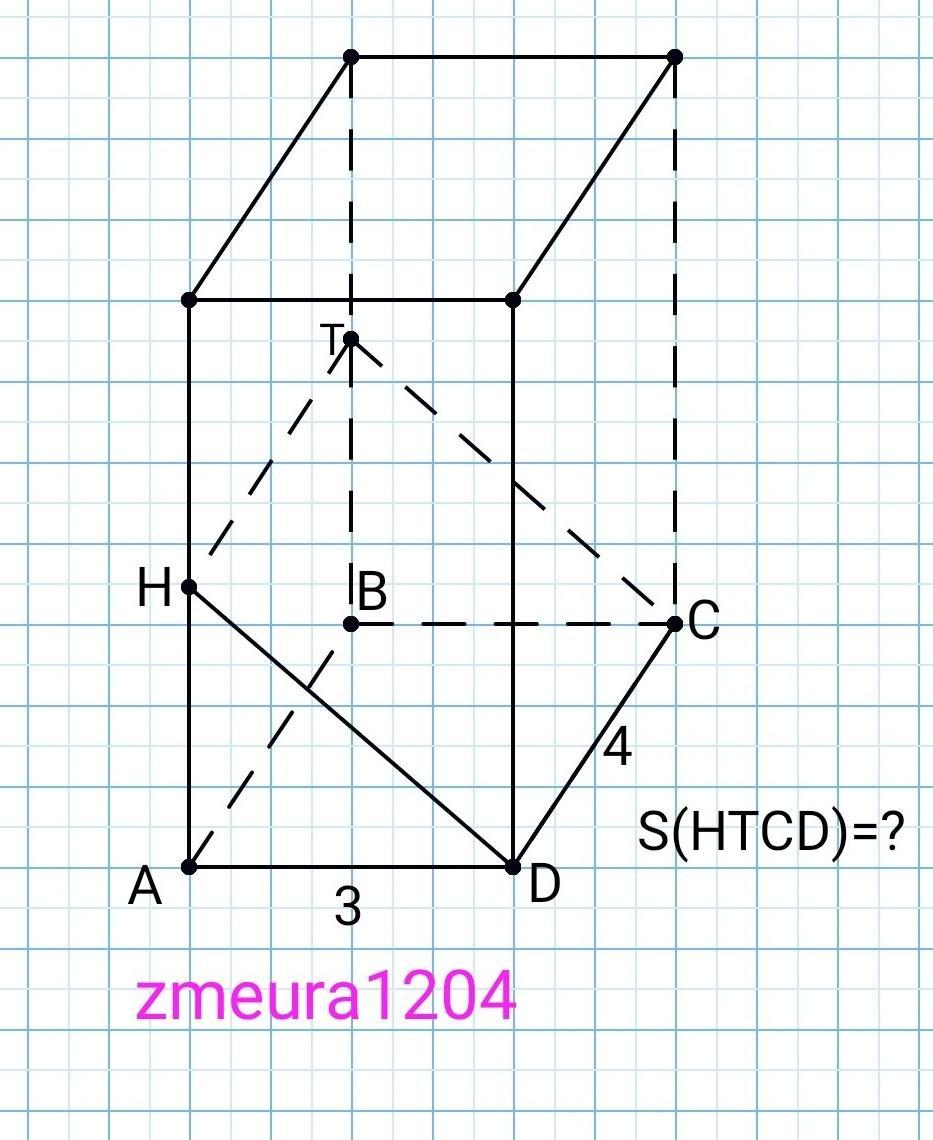
2)
S(ABCD)=AB*BC=3*4=12см²
S(ABCD)=S(HTCD)*cos30°
S(HTCD)*√3/2=12
S(HTCD)=12*2/√3=8√3 см²
___________
Приложения:
А почему Вы исчезли у меня из друзей? Это как так?
Не хватает маленькой феи, с палочкой!
Она улетела, но обещала вернуться.
Улетают, с обещанием вернуться, только Карлсон и Мери Поппинс.
:-P
А на малюнку 2 точно зображений
переріз паралелепіпеда площиною, що проходить через бічне ребро під кутом 30° до більшої бічної грані?
переріз паралелепіпеда площиною, що проходить через бічне ребро під кутом 30° до більшої бічної грані?
Ну, тогда S(CDD1C1)=4,8*4=19,2; S(HTCD)=19,2*cos30°=19,2*√3/2
Я извиняюсь за навязчивость, а почему S(HTCD)=19,2*cos30 а не разделить? Как в первом решении? Я не умничкю, я просто решать ее замучился
да.разделить.
отметьте нарушение,я исправлю.
Похожие вопросы
Предмет: Українська мова,
автор: arina176818
Предмет: Математика,
автор: adibaniyazova51
Предмет: Українська мова,
автор: aleksandrkiforenko17
Предмет: Русский язык,
автор: aknur140520
Предмет: Английский язык,
автор: Аноним
а) угол наклона диагонали параллелепипеда к плоскости основания;
б) площадь сечения параллелепипеда плоскостью, проходящей через боковое ребро под углом 30° к большей боковой грани.