Question

ОЧЕНЬ СРОЧНО, умоляю кто-нибудь

Методами диференційованого числення провести дослідження функції у=f(x) та побудувати її графік
y=-1/2x^3+6x-1
1.Знайти область визначення функції.
2. Знайти асимптоти графіка функції.
3. Знайти інтервали монотонності функції та локальні екстремуми.
4. Знайти інтервали опуклості та вгнутості графіка функції і точки
перегину.
5. Результати досліджень звести у підсумкову таблицю.
6. За підсумковою таблицею побудувати графік функції

Answer 1

Ответ:

См. решение.

Пошаговое объяснение:

Методами дифференцированного исчисления провести исследование функции у=f(x) и построить ее график

y = -1/2x³ + 6x - 1

1. Найти область определения функции.

x ∈ R

2. Найти асимптоты графика функции.

Функция непрерывна.

Вертикальных асимптот нет.

Наклонная  у = kx + b

$\displaystyle k= \lim_{x \to \infty} \frac{f(x)}{x}= \lim_{x \to \infty} \left(-\frac{1}{2}x^2+6-\frac{1}{x}\right)=\infty$

⇒ наклонных асимптот нет.

3. найти интервалы монотонности функции и локальные экстремумы.

Найдем производную, приравняем к нулю и найдем корни.

$\displaystyle y'=-\frac{1}{2}\cdot3x^2+6=-\frac{3}{2}x^2+6$

$\displaystyle -\frac{3}{2}x^2+6=0\\ \\12-3x^2=0\\\\(2-x)(2+x)=0\\\\x = 2;\;\;\;\;\;x=-2$

Отметим их на числовой оси и определим знаки производной на промежутках.

$---[-2]+++[2]---$

• Если "+" - функция возрастает, если "-" - функция убывает.

⇒ функция убывает на промежутках: (-∞; -2], [2; +∞);

функция убывает на промежутке: [-2; 2]

• Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке  - минимум.

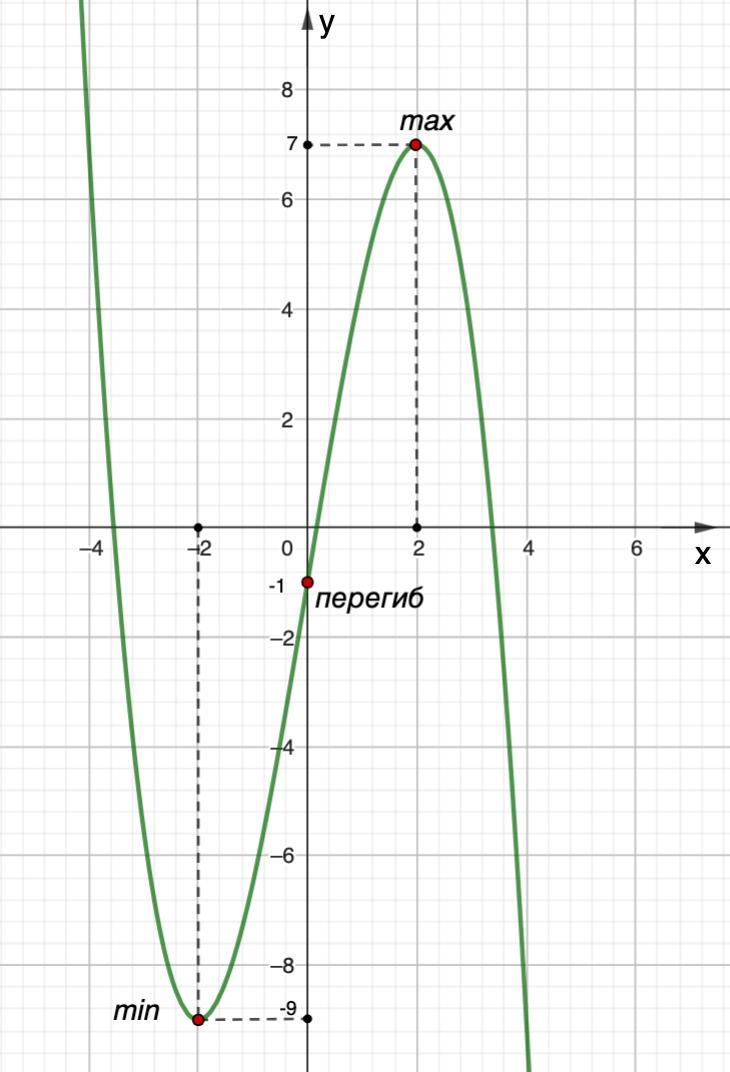
⇒ x min = -2;     x max = 2

y(-2) = -9;     y(2) = 7

4. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.

Найдем вторую производную, приравняем к нулю и найдем корни.

y'' = -3x   ⇒   x = 0

Отметим их на числовой оси и определим знаки второй производной на промежутках.

$+++[0]---$

• Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.

⇒ функция вогнута на промежутке: (-∞; 0],

функция выпукла на промежутке: [0; +∞)

х пер. = 0

у(0) = -1

5. результаты исследований свести в итоговую таблицу.

1) Монотонность:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c|c| c|}\cline{1-6}x& (-\infty;-2] & -2(min) & [-2;2]& 2(max) & [2;+\infty) \\\cline{1-6}y'(x)& - & 0 & +& 0 & - \\\cline{1-6}y(x)& \searrow & -9 & \nearrow & 7 & \searrow \\\cline{1-6}\end{array}$

2) Выпуклость, вогнутость.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c| }\cline{1-4}x& (-\infty;\;0] & 0 & [0;\;+\infty) \\\cline{1-4}y''(x)& + & 0 & - \\\cline{1-4}y(x)& \smile & -1 & \frown \\\cline{1-4}\end{array}$

6. по итоговой таблице построить график функции

Cм. вложение.