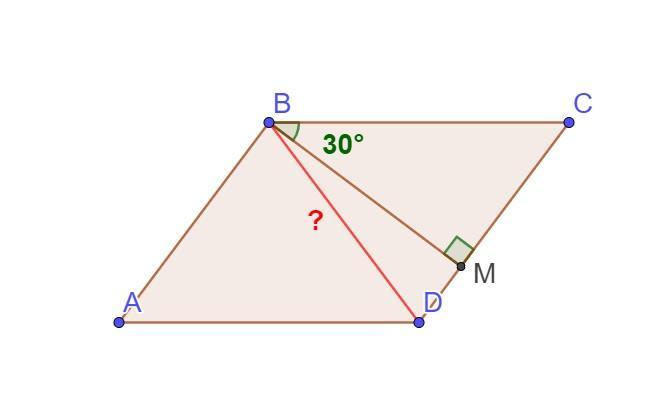
З вершини тупого кута В ромба ABCD проведено висоту ВМ до сторони DC, кут СВМ=30. Знайдіть меншу діагональ ромба, якщо його периметр дорівнює 32 см.
Ответы
Ответ:
Менша діагональ ромба дорівнює 8 см
Объяснение:
З вершини тупого кута В ромба ABCD проведено висоту ВМ до сторони DC, кут СВМ=30°. Знайдіть меншу діагональ ромба, якщо його периметр дорівнює 32 см.
Нехай маємо ромб ABCD, Р(ABCD)=32 см, ВМ⊥DC, ∠СВМ=30°.
Знайдемо ВD.
1.
Оскільки ромб – це паралелограм, у якого всі сторони рівні, то
АВ=ВС=СD=АD=Р(ABCD) ÷ 4 = 32 ÷ 4 = 8 (см)
2.
Розглянемо прямокутний ΔВСМ (∠ВМС=90°) .
За теоремою про суму гострих кутів прямокутного трикутника, знайдемо ∠С:
∠С = 90° - ∠СВМ=30° = 90° - 30° = 60°
3.
Так як у ΔВСD ВС=СD, то він рівнобедрений з основою ВD.
Отже ∠СВD=∠СDВ - як кути при основі рівнобедреного трикутника.
За теоремою про суму кутів трикутника маємо:
∠СВD=∠СDВ = (180°- ∠С) ÷ 2 = (180° - 60°) ÷ 2 = 60°
Отже, ΔВСD - рівносторонній.
тоді ВD = ВС = СD = 8 см.
Відповідь: 8 см
Відповідь:на фото
Пояснення:
