Предмет: Алгебра,
автор: zefirk79
Виконати дії ( з повним рішенням)!
Приложения:
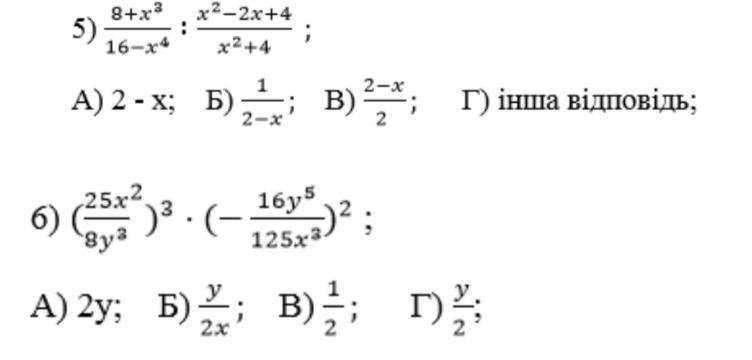
dimasprykhodko2332:
Знаю тільки другий приклад.
Добре пишіть тоді
Можете відповісти хоча б на 2 приклад
Встиг побачити відповідь? Її видалили. Якщо ні, то я продублюю
Так я встигла але не потрібно вже
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Здравствуйте. Помогите пожалуйста очень срочно, если сможете конечно же!
https://znanija.com/task/53777737
https://znanija.com/task/53777737
Прикольно. А мій варіант видалено
Тому що напевно ви невірно вирішили
Похожие вопросы
Предмет: Английский язык,
автор: tohirbekovaosiyo0801
Предмет: Английский язык,
автор: muratovazansaa50
Предмет: Физика,
автор: EliviAdi
Предмет: Английский язык,
автор: vfilimonova157
Предмет: Русский язык,
автор: kosovakata369